Please answer these questions.......please!!!

A cylindrical vessel of area of cross section A and filled with liquid to a height of h1 has a capillary tube of length l and radius r protruding horizontally at its bottom.If the viscosity of liquid is \eta and density roh \rho then the time which the level of water in vessel falls to h2 will be.
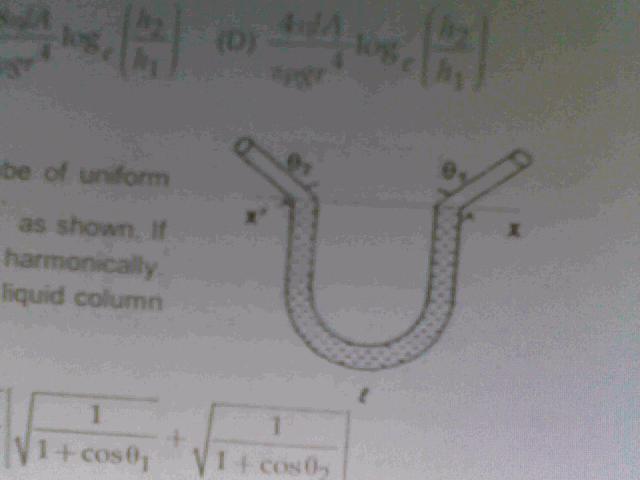
A liquid of density roh \rho and mass m filled in a U tube of uniform cross sectinal area.Initially the liquid is upto XX' as shown.If the liquid level is slightly displaced.it oscillates simple harmonically.The time period of oscillation wil b (the total length of liquid coloumn is 'l' as shown)
-
UP 0 DOWN 0 1 5

5 Answers
Here the SHM takes place with one frequency when the liquid rises through the right limb and with another frequency when it rises through the left limb.
Let's find the time taken for the liquid to move from the mean position, rise through the right limb and back to mean position (i.e. half the time period for the oscillation)
Now, since both open surfaces of the liquid is at atmospheric pressure, we can omit the effect of pressure in our analysis.
Let the liquid get displaced by x. Then the potential energy of the system is
\underbrace{\frac{\rho A(l-x)^2g}{2}}_{\text{for the liquid in the left limb}} + \underbrace{\frac{\rho A l^2g}{2}}_{\text{right limb vertical portion}} + \underbrace{\frac{\rho Ax(l+\frac{x \cos \theta_1}{2})g}{2}}_{\text{right limb angled portion}}
And the kinetic energy is \frac{1}{2} \times (2 \rho lAv^2)
So the total mechanical energy is:
E=\frac{\rho A(l-x)^2g}{2} + \frac{\rho A l^2g}{2} + \frac{\rho Ax(l+\frac{x \cos \theta_1}{2})g}{2} + \frac{1}{2} \times (2 \rho lAv^2)
Since it is a constant we have
\frac{dE}{dt}=0
which yields
a =- \frac{g(1+\cos \theta_1)x}{l}
Now, its easy to see that the time period of motion is
\pi \sqrt{\frac{l}{g}} \left[\frac{1}{\sqrt{1+\cos \theta_1}} + \frac{1}{\sqrt {1+\cos\theta_2}} \right]
You can also do the problem by looking at the restoring force. Here the liquid is restored to its mean position solely by the force of gravity.
If we again consider the situation when the liquid is moved by an amount x towards right. We consider an unconventional axis which runs through the length of the liquid instead of x-y axis.
Seen this way, the force of gravity on the left limb is forcing the liquid to the right and this force is \rho A (l-x)g
The compensating forces are
(1) weight of liquid in right limb =\rho A lg and
(2) component of weight of liquid in the angled portion along our axis
=\rho A xg \cos \theta_1
Hence the net restoring force is \rho A xg \cos \theta_1 + \rho A lg - \rho A(l-x)g = \rho Ax(1+\cos \theta_1)g and the rest is on the same lines as above.
PS: @shubham, could you please print these out for meethi?