Superb Gravitation problem by FIITJEEâ™ â™ â™ Help me!!

Let us consider the gravitational field strength of this hypothetical planet as " g " .

Then , according to Gauss ' s Law : -

∫ g . dS = - 4 π G M_enclosed

Now imagine a Gaussian cylinder of height " H " enclosing a portion of the planet as shown in the figure .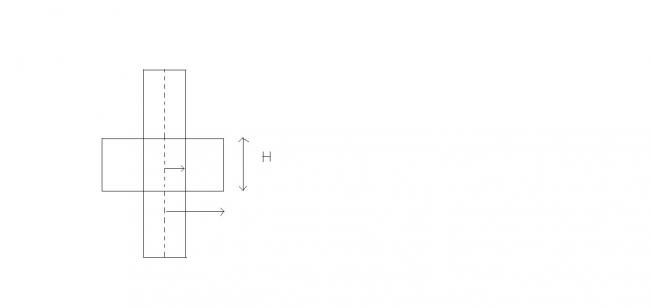

Obviously , the mass enclosed in this imaginary cylinder , M_enclosed = ρ . ( Ï€ R ² H ) .

The surface area of the imaginary cylinder , S = 2 π . ( 2 R ) H = 4 π R H .

Since , " g " in this case is cylindrically symmetrical , hence , we can take this factor out of the integration to obtain : -

g . S . cos ( 180 ° ) = - 4 π G M_enclosed

Or , g S = 4 π G M_enclosed

Or , g . 4 Ï€ R h = 4 Ï€ G ρ ( Ï€ R ² H )

Or , g = G ρ π R

Now , if we let the mass of the satellite be " M " , the orbital velocity being " V " , then : -

M V ²2 R = g . M = G M Ï€ ρ R

Or , V = R √ 2 G Ï€ ρ .