1Yah thnx
A particle B of mass 0.6 kgslides down the smooth face of a wedge A of mass 1.7 kg, which can move freely on a smooth horizontal surface. Inclination of the face to the horizontal is 45° . Then :
a) acceleration of A is 3g/20
b) vertical component of acceleration of B is 23g/40
c) horizontal component of the acceleration of B is 17g/40
d)none of the above
-
UP 0 DOWN 0 3 7
7 Answers
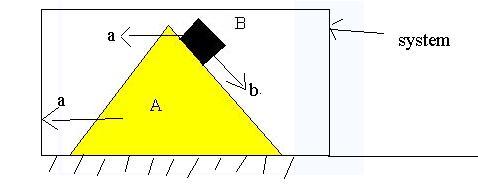
21let a => accel of wedge
b=> accel of block B wrt wedge
mass of wedge be w
mass of block be m
taking block and wedge as a system and applying newtons laws in horizontal direction
Fx=m1a1x + m2a2x =0
0=wa + m(a-bcos theta)..........i
using newtons second law along the incline plane and fbd of block
mgsintheta=m(b-acos theta).............ii
now solvie eq i and ii....(i will not solve those) :P
in vector form
awedge=a i cap
ablock=(a-bcostheta) i cap - b sin theta j cap
66Let M = 1.7 kg, m = 0.6 kg
On A, parallel to the horizontal a force N cos 45° acts towards the left. Here N is the contact force between A and B which acts perpendicular to the face of the incline. So if a0 be A's acceleration towards the left, then
N sin 45° = M a0 ----- (1)
Taking the reference frame as the wedge A, the forces acting on B are:
mg vertically downwards,
N perpendicular to the face pushing B away,
the pseudo force ma0 towards the right.
In this reference frame, B slides down the incline. So we have
mg sin 45° + ma0 cos 45° = ma' -----(2)
(here a' is the acceleration of B w.r.t. A)
Normal to the face: mg cos 45° = N + ma0 sin 45° -----(3)
Solving for a0, a' we get
a0 = mm+2 M g = .64 g =320 g
And a' = √2 (m+M)(m+2M) g = 23√240 g
Hence, the vertical component of B's acceleration is a' sin 45° = 2340 g
And the horizontal acceleration of B:
a' cos 45° - a0 = 2340 g - 320 g = 1720 g
So a), b), c) are correct.
1uc an solve it from the earths frame......
using constraint equations
ab=awcos@
so this means that
mgcos@-n=ma/√2
and
nsin@=Ma
or
66Of course, one can solve it from the ground frame entirely without reverting to any pseudo force. However, we must note that in the ground frame, the direction of B's motion won't be parallel to face of the wedge. In fact, the following vector equation holds:
\vec{a}_{BG}=\vec{a}_{BA}+\vec{a}_{AG}
(Here, aBG denotes the acceleration of the block B w.r.t. the ground, aBA is the acceleration of B w.r.t. A and aAG is the acceleration of A w.r.t. the ground.)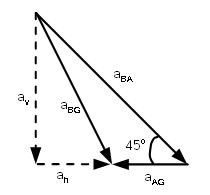
From the vector diagram, we have
\tan 45^\circ=\dfrac{a_v}{a_0+a_h}
where av, ah, a0 are, respectively, the vertical, the horizontal accelarations of B and the acceleration of A.
Further, the net horizontal force being zero, we get Ma0 = mah. These equations can be used to determine the required quantities in the ground frame.
1see sir from the ground frame i got another method to solve the sum.......
first let us assume that wedge was fixed then the mass would only move down the incline now since the wedge has a mass m the block will hv two acc one along the inclin and on perpendicular to it
considering th movemnt `perpendicular to it
this movement totall depends upon the acc of the incline so by applying constriant eq ........ ab=awsin@
now resolving forces in the pependicualr direction as we know that only presentln
n-mgcos@=masin@
and
nsin@=Ma
solving we get a or accleratiion of block as 3g/20
so the magnitude of block\s acc s 3g/20√2
its component in the vertical and horizotnal direction is also
3g/40 same in the vertical direction 3g/40
now for motion along the incline ..........
acc down the incline is gsin@=g/root 2
now taking vertical components the total adds upto g/2+3g/40 =23g/40
now in the horizontal direction the acc cancel so it comes up to g/2-3g/40
17g/40
simple