Means. that work accounts for the work ... It is a bit similar.. anyways
thanks
A body starts sliding (from rest) without friction down a hill of height h. In the beginning the body has potential energy and no kinetic energy; at the end the body has only kinetic energy. It follows from energy conservation, mgh=½mv2, that the velocity of the body at the bottom of the hill will be v=√2gh.
Now consider the same process from a reference frame moving with velocity v (to the right) relative to the ground (this is the same v as above). In this reference frame, the body in the beginning has potential energy mgh and kinetic energy (1/2)mv2, while at the end of the process both energies vanish.
Where did the energy disappear? Give a detailed account of missing energy!
-
UP 0 DOWN 0 2 30

30 Answers
possible hint i can give you here is,
See the normal force exerted by the wedge on the block from the ground frame. Angle it makes with ds at every instant. See the angle your normal force would make with the new motion ds' at every instant in wrt the new frame. judge for your self.
cheers!
@Ashish Bhaiya,
Now since you have revived it, I would like to say something on it. i.e., My faulty explanation :
In initial case, as said the frame i.e., the observer is moving with a certain velocity ' v ' in a direction. Hence the Block possesses energy given by mgh+1/2 mv2.
Now as the block slides down the hill and gains some velocity the observer sees that he's slowing down and doing some work against some external force that is acting on him. Over the time, when the block finally starts moving with velocity 1/2 mv2 , the observer sees that he has been completely stopped due to the external force doing work on him.
Hence, that dissipated energy as seen by the observer should have been utilized to create the above scenario to him.
[Sorry if I didn't read the earlier posts completely]
hey philips thast ok
but wat about a mathematical proof ?
in other words if the question is reconstructed :
"prove that the work done my normal force is 2mgh " ?
Oh I read it the thread should be closed.
#16 should do it unless Sir wants to add something more.
Is the thread still open ? sorry cant read through all the posts above.
I dont know how I missed this question when it was posted.
kaymant/nishanth/theprophet sir please can u provide the final answer
qualitatively wat rpf has told seems right , but is ther any proof
@RPF
yeah i understood wat u r saying
m pointing out the incorrectness in grammar of ur last sentence
vanishing energy is itself the work done!!!
1:Sir please tell me the diagram you have drawn is correct or that i have drawn.(BECAUSE YOU HAVE TOLD THAT RELATIVE VELOCITY BECOMES ZERO.)
2:Sir you have said ,"The law of mechanical energy conservation is valid in all reference frames. The initial and final values of the energies may be different in different reference frame." its true and i agree with that. so how can we say that energy at the bottom vanishes since conservation of energy has to hold good and at the top position the system has some non 0 energy.
3.the same thing i have shown in my solution so why my solution is incorrect.
@organic
this is my attempt to explain y work is done
actual definition of WORK is
"change in Kinetic Energy"
u may argue it is the displacement caused due to force
bt W=F. dS is a mathematical equation for work done n not its actual definition!!!
@kaymant sir...ya correct...just read the theory....PE is point dependent function
@organic...work is definately done...m srry i cant explain by typing
@RPF
ya i think its correct...bt i think ur last sentence "so the block is doing some work on the hill which is exactly equal to vanishing energy".....is partly correct!!!
the work done by block is itself the vanished energy
its not EQUAL to the vanishing energy!!!
isnt it??
ok
answer
the the energy doesnt vanish
infact in our new frame the hill is moving
so the work done by normal force aint 0
so the block is doing some work on the hill which is exactly equal to vanishing energy
sir i am talking about the #7
in #9 i have (according to me) tried to clarify #7
#8 is my contradiction to ut10's first post(which he has deleted now)...yes it is the question itself!!
@buddyboyy
P.E. has nothing with do with the velocity.
@organic
I am not sure about what you are trying to say in #9, and #8 is just the question itself.
well i dont hav any mathematical explanation for this yet
bt if the frame of referance is itself moving...with the same vel as that of the particle...the particle with respect to the frame of referance will remain at rest....bt the body n frame w.r.t ground will be moving with a velocity v...
since the body is at rest w.r.t. the frame of referance...it will not possess any KE
bt in real world (w.r.t. ground) its moving with a velocity v...so it does not possess any PE
hence both the energies vanish...
btw i m myself not sure abt this explanation n think sumthin is wrong...sum1 plz point out the mistakes in my explanation!!!
guys,
the energy of the block in the new reference frame does vanishes. Because, at the bottom its velocity zero w.r.t. the new frame we have taken. You just have to explain the disappearance.
P.S. The law of mechanical energy conservation is valid in all reference frames. The initial and final values of the energies may be different in different reference frame. However, the change in energy remains the same in all reference frame.
to clarify my posts...i am posting the figures,,
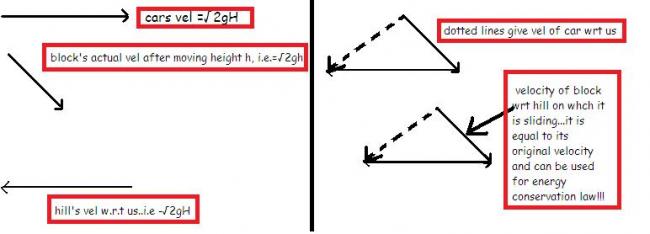
i feel this will clarify all doubts....[1]
@#5::
i feel it is a bit faulty...
the things i question...
when we are in ground frame of reference, the initial energy=mgh
final energy=12mv2
so equation=> mgh=12mv2
i do not get ur equation...
second case::
apparently the block moves back wid velocity v(same as v of car) and it is at height h
so total energy=mgh+12mv2
but as the block reaches final position, it is actually moving in same direction wid same speed as we are and so, it seems that it is at rest....
thus final energy seemingly is 0!!
but my solution contains something purely extracted from my imagination...
all such energy related problems will get solved only if we measure the energy values wrt the reference with whch our object mass is in contact that is the hill in this case!!
so when we are measuring with respect to hill from ground reference,
we say the vel is the vel of ball minus vel of hill(whch is now 0)
and when we see from a car , initially the ball and the hill moving in same direction with same vel...so relative velocity is 0
again while mass moves down slope then we find the relative velocity(vectorially)
if we do this then we will see that the problem of LOSING energy is magically solved!!
let us take the situation with reference to the ground.
then
total energy at top position is mgh
since surface is frictionless and velocity of the center of mass of the system initially is 0.
hence mv1 =Mv2
by applying conservation of energy
12mv12+12Mv22=mgh .........eq1.
now the situation with respect to inertial frame moving with velocity v.
we apply conservation of momentum as
mv+Mv=m(v-v1)+M(v+v2)
=>mv1=Mv2;
now total energy at the top position is
mgh+12mv2+12Mv2 ............eq2
total energy at the bottom is
12m(v1-v)2+ 12M(v2-v)2=12mv12+12Mv22+12mv2+12Mv2=12mv2+12Mv2+mgh (from eq1)..........eq3
since eq 2=eq 3 hence conservation of energy is satisfied.
ut10 assume that velocity at lowermost point is in horizontal direction
and the relative velocity becomes 0!!!!!
HINT(may be ):the hill is also moving in new frame
No... its entirely within the framework of Newtonian mechanics.
P.S. You should have a look at the mechanics questions that I have asked in the past. They are grounded to the physics as given by Newton.