1@swordfish, i m not able to understand ur figure properly....
how can the length of the string be (2 + √3)a ??
what is the ans??
A particle of mass m is attached to one end of a light elastic string of natural length a and force constant mg/a. The other end of the string is attached to a fixed point X. If the particle is released from rest at X, find time that elapses before it returns to X.
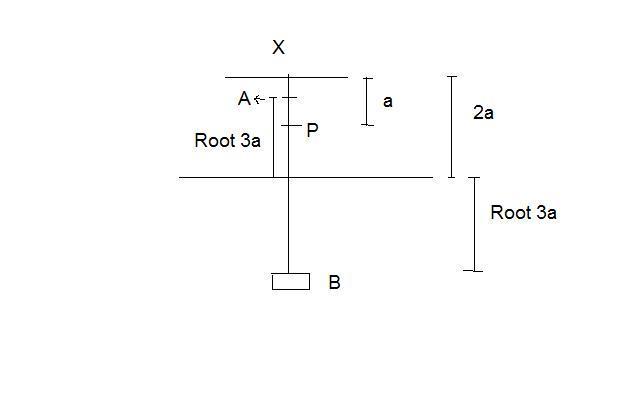
Refer figure.
I got the time taken from X to P and P to X.
The problem I am facing is the time taken to travel P to B and back
I got the equation of SHM as
x=Asin(ωt + ∂) where A = √3a and ω = √(g/a)
at t = 0 let x = a so that sin∂ = 1/√3
The particle will be again at P after time (say T)
a = √3a sin(ωT + ∂)
sin∂ = sin(ωT + ∂)
∂ = π - (ωT + ∂)
T = 1/ω ( π - 2arcsin( 1/√3 ) )
In the solution he got T = 2/ω (π - arccos(1/√3))
Moreover, he took the equation in terms of cos (Not sin) and he too took t = 0 at x=a
How can the two times taken be different no matter what equation you take???
-
UP 0 DOWN 0 0 5
5 Answers
11i think it is a simple one..
Point X is apoint of max compression and hence a point of extremum.
time taken to reach same extreme = Time Period of Oscillation
also ω = √k/m = √mg/am = √g/a
so T = 2Π√ag
1No Euclid you are wrong.....
length of the string can be (2 + √3)a when it is stretched.
The asnwer is T = 2√2a/g + 2√a/g(Π- arccos(1/√3))
I got the first term of the expression but don't have a clear idea about second term.
I m getting the second term as √a/g ( π - 2arcsin( 1/√3 ) )