:) OK...lets see it this way...
When you draw the FBD of m2...no spring force comes into action. Acc. of m2 will depend only due to forces acting on it. The system boundary does not contain the spring.
1. Rolling Question :
A sphere S rolls without slipping mving with a constant speed on a plank P.The friction between the upper surface of P and the sphere is sufficient to prevent slipping , while the lower surface of P is smooth and rests on the ground.Initially ,P is fixed to the ground by a pin N.If N is suddenly removed :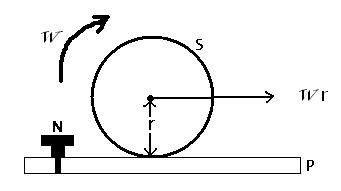
[A] S will begin to slip on P
[B] P will begin to move backwards
[C] The speed of S will decrease and its angular velocity will increase
[D] There will be no change in the motion of S and P will still be at rest.
Answer given : [D] !
IMPORTANT POINT / DOUBT : I just cant understand where the reaction (of the friction force on the sphere) acting on P vanishes , why is it not able to make P move ??? [7]
2.Extremely BASIC question from Waves [I'm poor at Mechanics :( ]
A string of length L is stretched by L /10 and the velocity of transverse wave along it is v .When it is stretched by L/20 [assuming Hooke's Law is applicable ] , the velocity of wave will become :
[A] v
[B] √2 v
[C] v√2
[D] 2v
Answer given : [C ]
IMPORTANT POINT / DOUBT : This answer will come if we use the relation v is directly proportional to √T [ T: Tension , v: velocity] and then proceeding by Hooke's law..BUT how can we say that v is directly proportional to √T when length of the medium changes ?? [7]
3.ANOTHER DOWN TO EARTH BASIC QUESTION from Laws of Motion :
In the figure given below ,the spring ,the pulleys and the strings are all massless.The pulleys are frictionless at their axles and it is given that m1> 2m2.The system is initially in equilibrium and the string connecting m2 to the rigid support below is now cut.The initial acceleration of m2 immediately after cutting the string will be :
Figure :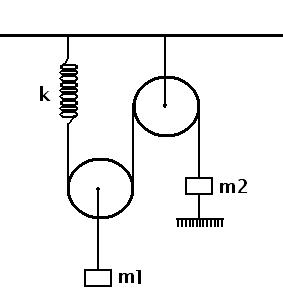
[A] (m1-2m2)2m2 g
[B] (m1-m2)m2 g
[C] (2m1-m2)m2 g
[D] (m2-m1)m2 g
Answer given : [A]
MY DOUBT: HOW ?..PLEASE GIVE FULL STEPS..PLEALSE !
-
UP 0 DOWN 0 0 23

23 Answers
In 1st question as the the sphere is moving with constant speed so no acceleration and so no friction is acting on the body
ok..buddy boy..thanks..if u have time then pls solve the other ones too..[atleast one ]
@jsg...
i agree with ray on the rolling friction thingy
i hav not done rotation yet....bt i asked my prof abt how n y a body in pure rolling in a body stops??
he said...in physics we consider every body to be 100% rigid...bt in reality no body is 100% rigid...so wenever it rolls...it gets slightly deformed...hence the rolling friction acts
bt its true that rolling friction is so small that it is neglected!!!
so ray said it right....ur reasoning is correct bt not arguable!!!!
Thanks Ray , but can you just tell whether you also did Q.2 by the same way [v is directly proportional to √T ] ?
Q1) Rolling friction is so very small that it can be ignored. Ur reasoning is correct...but not arguable.
Ok..Ray..:)..I'm 60 % convinced..I think I dont want to waste ur time [seriously..bcoz dont get addicted ]...i will let that ques go..just tell me abt 2 and 1 yaar..u will be doing a big favour on me..
@ Ray : for question 2 :
v=√T/μ , rt ?..here μ=m/L
So actually L changes..then how can we take : v is directly proportional to √T ??
[ I'm not sure with this concept , so maybe I'm telling the wrong thing ]
Bhaiyya...that is the point I want to put across. Agreed that the acc. of m2 is dependent on every factor...but do we ever show it in a FBD. We only account the force acting on the body. The beauty is wen u draw a FBD, it includes the effect of other factors.
But acceleration of m2 depends on tension which in turn depends on -kx also [not just -kx but even acc of m1 also ]
I CANNOT BELIEVE IT..NOT EVEN A SINGLE REPLY IN TARGET IIT , THAT TOO THE QUESTIONS ARE VERY BASIC AND NOT A SINGLE SOUL IS REPLYING..THE CONDITION OF TIIT IS CERTAINLY DETERIORATING AND THIS WAS EXACTLY WHAT HAPPENED AT GOIIT..[2][11][200]
hm..thats a good idea..but frankly Ray , I must say that it is not convincing [ what can I do ? ] because though the spring resists elongation , in cases like these the FORCE -kx HAS TO ACT , AND IF IT ACTS , IT WILL COME IN THE ANSWER..
The elongation? If m2 accelerates upwards how would the spring elongate?
I haven't done laws of motion for a while...even simple problems are not striking me as they should.
#6
Y shud spring be given in the answer? I thinh you missed out on this part "immediately after cutting the string". The spring will resist the elongation. Thats its property....just like an inductor resist change in flux when a current is switched on.
I think..you made some mistake in the tension part..BUT I'm sure in these parts..my only doubt is why the hell is the spring not being used..and the main doubt : the ans comes only when we consider some equations of equilibrium [ WHICH U DID AND I THINK IS ALSO WRONG ]..because after the system starts motion i frankly think that there is absolutely no use of the static equations..
In equilibrium,
FBD of m2 :
T = m2g + Support
FBD of m1 :
T = m1g
After the rigid support is cut, as m1 is definitely greater than m2, I figure m2 would accelerate upwards.
T - m2g = m2a
=> m1g - m2g = m2a
=> m1g - m2gm2 = a
What exactly did I miss?
@ Pritish , to get the answer [that they tell] , first use equilibrium condition and then simple force equations , BUT THE SURPRISING THING is that the spring doesn't even figure in the solution..then why exactly is it given , just for confusion..!! ?
I'm weak in physics but...do we have to use constraint equations in last question or will force equations be sufficient?
@ Anirudh , something called 'Rolling friction' does exist though its magnitude is about 100 times smaller than the usual magnitudes of static friction . This rolling friction has to be present in order to make rolling possible and to sustain it..[as far as i know ]
1) that is so because the sphere is already in perfect rolling without slipping .so no firctional force acts.
i.e the bottom part of sphere is already in rest w.r.t the plank. thus there is no horizontal force for the system thus no affect of removing the pin.