A chain of length l and mass m lies on the surface of smooth sphere of radius r > l with one end tied to the top of the sphere.(a) Find the gravitational potential energy of the chain with reference level at the centre of the sphere.(b) Suppose the chain is released and slides down the sphere. Find the kinetic energy of the chain, when it has slid through an angle θ.(c) Find the tangential acc. dv/dt of the chain when the chain starts sliding down.
-
UP 0 DOWN 0 0 1

1 Answers
(a) Just take a small section, find its PE & integrate it
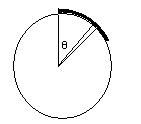
Mass of that small section dm = m/l * r * dθ
Height of that small section above center of sphere = r cosθ
PE of that small section dE = dm * r cosθ * g
=> E =∫ dE = mr2/ l * sinθ
Limit is from θ=0 to θ=l/r
=> E = mr2/ l * sin(l/r)
I think this was pretty much simple [1], try to solve b and c from urself.