zero... in an inertial frame pseudo forces are not considered..
a particle is observed from an inertial frame of reference and it is found to move on circular path of radius r with a uniform speed v The centrifugal force on the particle is ??
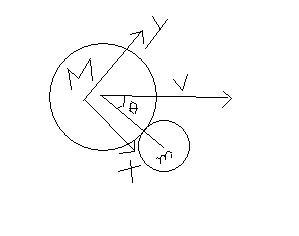
a ball of mass M strikes another ball of mass m at rest If they separate in mutually perpendicular directions then the coefficient of impact (e) is
Please solve them
-
UP 0 DOWN 0 0 4

4 Answers
from figure...
Mvcosθ = Mv1 + mv2 ... (i)
and
v2-v1 = evcosθ ... (ii)
Solving these two..
v1 = (M-em)vcosθ/(M+m)
and v2 = Mvcosθ(1+e)/(M+m)
looking at the coordinate system that i have taken,
VM initial = vcosθ i + vsinθ j
VM final = (M-em)vcosθ/(M+m) i + vsinθ j
Vm final = Mvcosθ(1+e)/(M+m) i
Now, Vm final and VM final are perpendicular, so this is possible if i component of VM final = 0,
and as cosθ≠0 as i of both final velocities will become zero,
hence M-em = 0 ==> e = M/m