71If anyhow you can assert it. i too did the sum the very same way. also mention some hints or solve the first one. please
The free end of a flexible rope of Length L and mass λ per unit length is released from the rest in the position as shown in the figure (A). Determine the velocity V of the moving portion of the rope in terms of y.
-
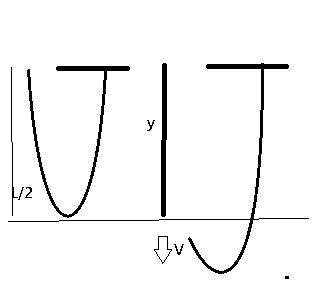
UP 0 DOWN 0 0 17
17 Answers
1yes we it makes a diff...
the only method to solve this sum is by dirty calculus thats y i am refraining give me sum time looks like maybe i have a new sol....
and the naswer 1/2sin.... is wrong...
71It was given just as I have posted. You may assume whatever you like and see if it matches with the conditions/answers!!
49are u sure the rope is in parabola form??
look....the dist frm point of suspension till lowermost end is half the total length...
forces me to think that the rope is nt in the way it is shown but instead it is kept in a way such the fixed half of the rope is coinciding with the rest half...
as a result of which the centre of mass resides at L/4 from the top...
11 st sum is simple calculus
the 1t rope is in the form of a parabola y=x^2
sinilarly for the other
calc the dirty integration and u get d answer...
71
23refer fig in # 3
working in frame of the sphere ( bcz in dis frame normal does no work , )
mgcosθ - masinθ - N = mv2R..(1)
Wg+ Wpseudo = ΔK
mgR(1-cosθ)+ maRsinθ = 12mv2
i.e mg(1-cosθ) +masinθ = mv22R...(2)
this vel is in frame of sphere
frm 1,2
and putting N = 0
2mg (1-cosθ)+2masinθ=mgcosθ - masinθ
i.e 2mg+3masinθ=3mgcosθ
2+3sinθ= 3cosθ (a=g)
i.e cosθ - sinθ= 2/3
frm 1
vwrt sphere = √ 2gR/3
( wat aniruddh did is correct , he just made one calc mistake somewhere )
71A body is placed on the top of a smooth hemispherical surface of radius r. The hemisphere is accelerated to right with accn a. Find the velocity V of the body relative to the surface at the time of losing contact. Find the angle φ if a=g, P is the point where the body loses the contact.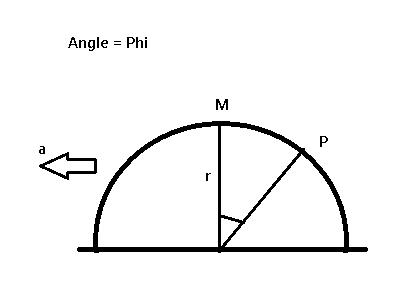
Problem: I tried all things, Pseudo force, Centrifugal force and all that but couldn't match the exact answer.
11st thing wpe can be applied coz work is being done on the block by he hemisphhere the n force work would have only been applied when the sphere is at rest....
71Also, The velocity v=\sqrt{\frac{12gR}{13}}.
Any clues?
71euclid. the angle given in the answer is 22.6 degrees. is ur answer evaluating to that?
1y???that should have matched....
apply a pseudo force to the body and put N=0 (at the angular position where it loses contact)...
i get answer as φ = sin-1(2/3) + Π/4 (assumed a=g)
