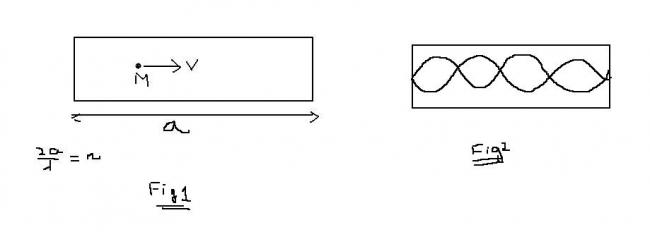
The wavelength associated with the matter wave is
\lambda =\dfrac{h}{p}
where p is the momentum
The allowed values of the momentum is determined by the boundary condition
a=n\lambda/2\quad\Rightarrow \ n\lambda = 2a
i.e. the allowed momenta are given by
p=\dfrac{nh}{2a}
Hence, the allowed energy states are
E_n=\dfrac{p^2}{2M}=\dfrac{n^2h^2}{8a^2M}\qquad n=1,2,\ldots
So the transition from the ground state to the next state requires an energy difference
\Delta E_{1\to 2}=\dfrac{3h^2}{8a^2M}
P.S. edited to make that a to a2