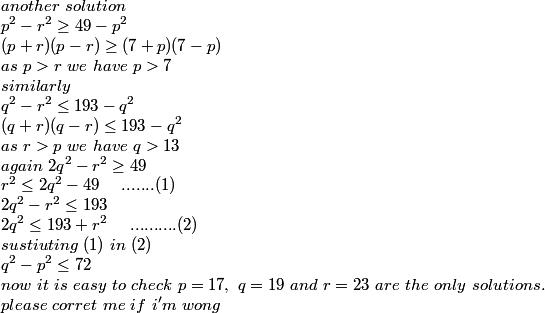1to find the three numbers you need to go methodically
then you will easily get the answer
the answer should satisfy initial conditions
Let p,q,r,be three prime numbers such that
5<=p<q<r
and
2p2-r2>=49
2q2-r2<=193
find p, q ,r
-
UP 0 DOWN 0 2 7
7 Answers
33p=7
q=11
is one of the soln...
r=7
[6]but it soenot satisfies initial condition...
11good work ,
but how do you know that this is the only possible combination?
1step1. prove that 2q2≤193++r2≤2p2+144. implying q2≤p2+72.
step2. 2p2≥49+r2>49+p2 implying p≥11.
step3. if p==11, r=13, not possible.
if p==13, r=17, not possible.
if p==17, we have found a solution.
let p>17 implying q>19 implying p+q>36 implying q2-p2>72 since q-p>2..
so p≤17. proved.
1good proof ..
i proved the same way
i wonder if there is any other way to prove it..
