yes i think because let area of larger square=n2 sq units
it can be divided into n smaller squares of area
1 sq unit + 3 sq units + 5 sq units + ... + 2n-1 sq units
such that their sum is = n2
Some of the university lecturers here were interested in the question:
Is it possible to divide a given square into n squares for any n≥6?
(Obviously all squares neednt be the same size)
-
UP 0 DOWN 0 1 16

16 Answers
example for n=7, n2=49
it can be divided into 7 squares of area
1 sq unit + 3sq units + 5 sq unit + ... + 13 sq units = 49 sq units
sir am i correct?
"here" meant where i stay :D
@fibonacci - no i meant like u can divide the square into 6 squares or 7 squares or any number of squares greater than 6.
Well? Heck this is not so tough. You need minimal maths background to be able to do this.
is it right way to proceed??
we could subdivide the square in 4, 9, 16 or ... squares, then subdivide them further etc.
this way you get every n with n = 1 mod 3, every n with n = 1 mod 8, every n with n = 1 mod 15 etc.
you can get every n such that n-1 is a sum of 3's, 8's, 15's, etc
this solves all n≥ 17
n=16 is clear
bhargav.. even though I did not understand your explanation "fully", I think what you are tryign to say (or what i am interpreting seems to suggest that you are correct. )
how do we explain n = 6 this way ?
also maybe n = 8 ?
[2] maybe i didnt get your method.
or is there a misprint in the question ?
Basically we need to confirm for cases 8,11 and 14.
Is that right prophet sir?
ya, first how to we go from the statement: "we can sub-divide into 4,9,16 squares ..." to "this way you get for all n = 1 mod 3 ..."?
next: from this point to "sub-division for every n≥17 is can be obtained this way"?
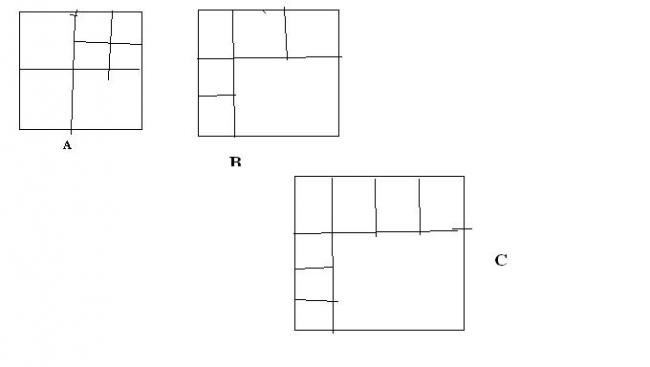
So, now if we keep on dividing the bigger square in each of the figures A,B,c in 4 parts, 3 additional squares get added during each subsequent division......So, that gives we can divde a square in n squares for all n≥6.
Yeah that's correct.
We first note that if you have a sub-division into n squares, you also have a sub-division into n+3 squares by choosing any one square and dividing it into 4 parts.
So if you find a division for n = 6,7,8 you would have proved for all n
n = 7 is easy because you can divide into n = 4 and so you can divide into 4+3 = 7
for n = 6, consider a 3X3 and then consider a 2X2 in it as one square. That gives you 9 -4+1 = 6 squares
for n = 8, consider a 4X4 and consider a 3X3 as one square. Now you have 16-9+1 = 8 squares and so we have proved for all n