1Yup.... it's a nice problem, with an elegant solution...
An equilateral triangle is divided into 36 smaller equilateral triangles by dividing each side into 6 parts and joining the corresponding points on adjacent sides of the triangle.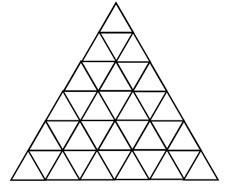
There is a drunk ant at each of the 28 vertices and they all start to walk along the edges (in random directions) with the same speed. Since they are drunk ants, they can't walk straight for too long and will change their direction (by ±π3 or ± 2π3) as soon as they reach the next vertex. Prove that eventually, there will be two ants at the same vertex.
-
UP 0 DOWN 0 1 6
6 Answers
106:P IITK Brainwaves question For 22 Sept. 2010
well new questions uploaded daily @ 2.00 pm (until takneek gets over)
http://students.iitk.ac.in/snt/takneek/competitions/brainwaves.php
341I could be missing something here, but however drunk the ant maybe, I could lead each ant back to its initial position in two moves. So, this sequence of moves avoids having two ants eventually at the same vertex.
106sir, could you post how
I could lead each ant back to its initial position in two moves. ?
341Oh heck! I overlooked the obvious physical constraint.
I feel the solution will have something to do with a result known as Sperner's lemma. Lemme see if I can formulate something on those lines