9can u explain it b555 ??
i had a careful look cudnt figure out :(
Here are the Questions i could remember .....
Q.1. What should be the values of x and y such that x2 + y2 is minimum and (x + 5)2 + (y – 12)2 = 142 ??
I got the answer as (x, y) = ( 5/13, -12/13 ) and min value as 1
Q.2. sorry i had written wrong Q here b4 ....
correct Qsn in post # 35
Q.3. If p is a prime number > 5, and its reciprocal can be written as
{the bar is over entire a1 to ar } where 
is the recurring part, prove that 10r on dividing by p leaves remainder 1.
This was the easiest of the lot.
Q.4. If a, b,c are odd integers, prove that the roots of ax2 + bx + c cannot be rational.
i proved that the Discriminant is of the form 8n + 5 .... so can't be perf. Sq That wud do?
Q. 5. There are six different paints given to you, and u have to paint all the faces of a cube with a different colour ….. In how many can this be done? {not sure but i think this was the Question}
Q. 6. A rectangle is inscribed inside a triangle of area M . What is the maximum area of the rectangle??
Is it M/2 ? Plz say yes
Q. 7. a, b, c , d are integers such that 
, b1 and b2 are integer multiples of ad – bc. Prove that the equations ax + by = b1 and cx + dy = b2 can have simultaneous solutions in integers.
Q. 8. Consider this sequence of natural numbers without the digit ZERO appearing in them : 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13,. ….. Find { an } . Compare this with a geometric series and prove that 
.
What is meant by the symbol {an} ?? [7] is it general term?
Q. 9. x, y, z are real numbers none equal to zero.
are complex numbers with 
.
If 
, prove that 
.
Q.10 in post # 35
-
UP 0 DOWN 0 3 50
50 Answers
9sorry b555 for being so unaware of the term multiplicity :(
i researched on this and found that a root has multiplicity of k if all its derivative till k-1th derivative are 0
now f(x) =x (x+1) (x+2) … (x+2009) - c
f'(x)= (f(x)+c) [ 1/x + 1/x+1 + ..... 1/x+2009 ]
let x be a root with multiplicity >2
now f(x)=0
f'(x)= c[ 1/x + 1/x+1 + ..... 1/x+2009 ]=0 (c≠0 has if c=0 ,clearly 2010 roots possible)
implies
now f"(x) =-c[ 1/x2+1/(x+1)2 +....1/(x+2009)2] ≠0
so maximum multiplicity =2
now when multiplicity =2
f'(x)=0
f'(x) is a polynomial of degree 2009 and has only one real root as f"(x)≠0
so only one value of c possible
9
39ok celeestine , see this
u say opposite pairs for paints are chosen in 6C2 . 4C2 = 90 ways
but no, thats wrong. its 90/6 [6=3!]
(because the three pairs are indistniguishable)
1@ q 5)... the same q is in MLkhana and the ans was 1...
the solved it as: 6!/6! (since the sides of a cube are similar!!)
whom to trust??
1My sincere apologies for posting wrong Question no. 2
Q. 2. This was the correct Question –
f(x) = ax2 + bx + c be a quadratic polynomial such that
f(-1), f(0), f(1) belong to [-1, 1].
Prove that 
Q. 10. For some fixed real constant c,
Prove that any root of the equation x (x+1) (x+2) … (x+2009) = c can have at most multiplicity 2.
Determine the number of values of 'c' for which the equation has a root of multiplicity 2.
392nd one is easy. u have 3 cnditions so use legrange interpolation to find the polynomial,. then at later stage u would have to solve triangle inequality. done
3910th one..........
hm this seems interesting. (that doesnt mean its a tough one)
waiting to see if anyone got a better soln
39celestine , are u joking or wat ?????????????????????/
a root is ssaid to be of multiplicity `k` if its k times repeated root.
like for x22+4x+4 , -2 is a root of multiplicity 2
for (x-1)2(x-2) , 1 is a root of multiplicity 2
i hope u get it
9b555 are u getting the ans for Q2.
uve said in #36 the Q is easy cud u show ur working ???
im getting only | f(x)| ≤ 3 :(
39this is my method (please dont laugh , as i couldnt find a better one)
begin by writing the polynomial in the form u(x-1)(x+1) + vx + w
then f(-1) = -v + w, f(1) = v + w, f(0) = w - u
there is a formula describing f(x) in terms of f(-1), f(0), f(1)
because a quadratic polynomial is fixed by giving any three of its values (at different points)
google for "lagrange interpolation" if you don't know the formula,
i mean, if f(-1), f(0), f(1) are known then you have a linear system of equations on a,b,c
so it rema+ins to prove that if u,v,w are in [-1,1]
(U = f(-1), V = f(0), W = f(1))
then
|V(1-x^2) + U/2 (x^2-x) + W/2 (x^2+x)| <= 3/2
triangle inequality on the LHS
remains to show that |1-x^2| + |x^2-x|/2 + |x^2+x|/2 <= 3/2,
which is easy to prove
9for Q8
if an is nth term its easy to see
an = n +[n/10] +[n/100] +.....[n/10r]..
see #48 , #49 for part 2 ans :)
9waw terrific sol b555 :)
this was the only Q in ISI above jee level i think .
ur method is so tight u r infact proving modfx <= 3/2 - 1/4
9did u give the ISI b555 ?
and can u solve the Q8 also im not getting the Q at all see #44
39no cele , i did not give ISI. actually was thinking my math wasnt of that level.
1Ok here goes the solution to 8th
see that let us take an n digit number
total possible numbers = 9*10n-1
now let us consider the numbers with zeros
= n-1C19*9n-2+n-1C29*9n-3.....
+9
=n-1C0*9*9n-1+n-1C19*9n-2+n-1C29*9n-3.....
+9 -n-1C0*9*9n-1
=9*(1+9)n-1-9n
now total number of numbers without zeros = 9*10n-1-9*(1+9)n-1+9n=9n
now summation of number having n digits
1/10n-1+1/(10n-1+1)+....
now number of numbers we add = 9n
each number <1/10n-1
so we have sum <9n*(1/10n-1)
now number of digits varies from 1 to inf.
so sum ≤9+9*(9/10)+9*(9/10)2+....
<9 [ 1/(1-9/10) ] =90
9rohan why did u work so hard to get 9n ??
u can just do it as 9*9*9....= 9n as each digit can have 9 possibilities
11@Mirka
[10][10][10]
thank u for all the ques
ab thoda kaam karte hain [1]
Q1
look according to the question asked the min value of x2+y2 should be 0 as we can take (0,0)point
so the answer is 0
but respecting the question and understanding the mistake
it should be mentioned that the point lies on the curves
so
we can see that it cuts the coordinate axis at (0,-2) and (9,0)
we observe that the distance of (0,0) from (-5,12) is 13 so the line continuing shall have the distance of 14 at a distance of 1 from (0,0)
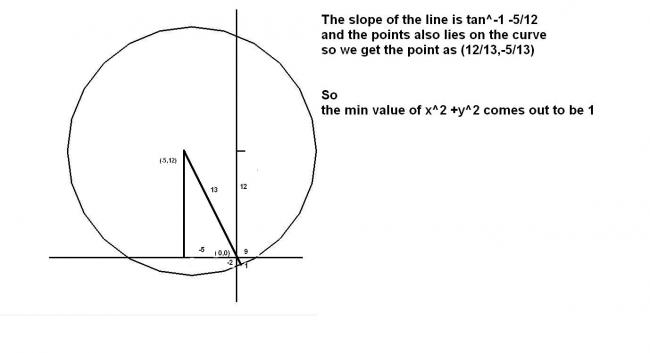
62this tyep we have done many times here..
this is the smallest distance from the center to the circle of radius 14 at point 5, 12
the answer will be 1 by geometry.
39and 8th q is a well known question. !!!!
i think most of u know how to do it