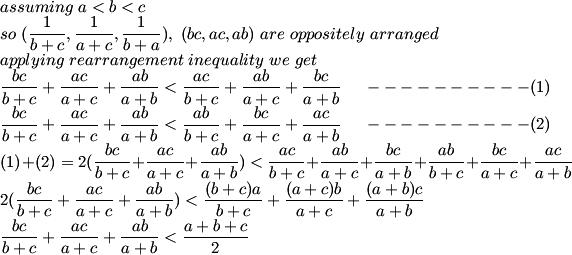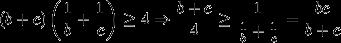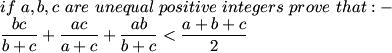The Diophantine eqn is quite easily factorisable.... (x-1995)(y-1995)=1995^2 - that directly gives the number of solutions.
here's a simple one
prove that a number with 3^m equal digits is divisible by 3^m
-
UP 0 DOWN 0 0 20

20 Answers
one doubt in # 12
the number f ways of resolving 325272 in two factors
shuld be (3C2)3=27
but rahul has written 27+1 / 2
y it shudnt be 27
second try was unsucceful.
anyway i wanted to write that from (b+c)(1/b + 1/c) ≥ 4 it follows
(b+c)/4 ≥ bc/b+c
Adding up the three inequalities formed this way gives us the answer
@theprophet
can you please convert your solution to .png format using paint as it is unreadable :D
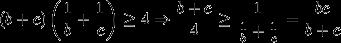
similarly we will have two other inequalities with a+b/4 and c+a/4 adding which we get the one in the question
If there r 3m repetitive digits x, then their sum will be x3m => Number is divisible by 3m.
P.S:
If wrong: Just kidding ;)
If right: Thank you
i think i should wait till tomorrow as there may be someone trying or should i post it now
@theprophet you are absolutely correct!
that was exactly how i had done ! :D
here's another one:-
find number of solutions in N*N to the equation 1/x+1/y = 1995
Induction is a dependable friend
For m =1, any such number is a multiple of 111 which is divisible by 3
Let us assume the truth of the statement for m = k.
i.e. the number Nk = nnn....nnn (3k times) is divisible by 3k
Now the number Nk+1 = nnn....nnn (3k+1 times) consists of 3 blocks of the number Nk
so Nk+1 = Nk [1+103k+102.3k]
The bracketed term is divisible by 3 and Nk is divisible by 3k and hence Nk+1 is divisible by 3k+1 which wraps up the induction process
but that's what you have to prove ie the divisibility test of numbers with 3^m equal digits. you have to prove its obvious :D