62
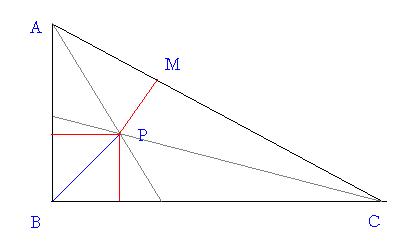
Now here P is the incenter..
so the three red sides are all 4√2
so BP=8
1i think that the question is incomplete
let us join B to M
let the feet of perpendiculars from P to the AB be D
then in triangle BMP ,√BPM=√DPB+√DPM
as ADPM is cyclic √DPM=180-√A
and further √BPD=45 (as it is right angle isoceles)
so we get by cosine rule in that triangle =>
cos(45+180-A) = (BP2+PM2-BM2)/2*BP*PM
as we already know BP and PM , to find BM we need to know cos(180+45-A) => to know angle √A
but with a fixed inradius ,(that's all given in ques) we will get varied values of A
so value of angle A should be known
62
Lokesh Verma
·2008-11-16 08:25:05
no there is no need for the requirement of the isoceles triangle.. check my method buddy!
62
Lokesh Verma
·2008-11-16 08:31:22
Do u see that P is the incenter? (incenter is the meeting point of angular bisectors)
Once P is the incenter, It is equidistant from the 3 sides!
So the three red lines are of equal length :)
Now the blue line (THe one whose length we have to find) is the diagonal of the square of sides of length red lines)
so the length is root 2 times the length of the red lines!
1
Rohan Ghosh
·2008-11-16 08:32:28
but in the question you mentioned that we need to find BM
62
Lokesh Verma
·2008-11-16 08:34:03
OOOOOPS>.. dude i din see that!
i just thought we needed to find BP..
sorry u are right..
