i think u know about my brother!!!!!
he is in delhi iit computer science M.Tech (Ashish Jindal ,AIR 223 IIT JEE 2007)
I remember Nishant Bhaiya's face when he was discussing this problem....well he hates this type of abstract problems but i love this one....
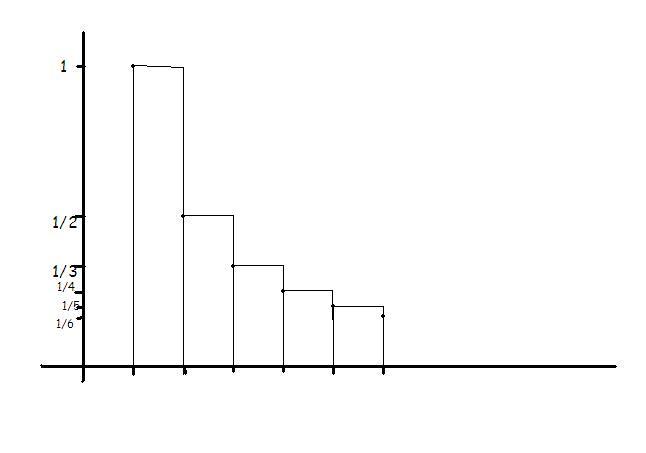
find the value of:\sum_{1}^{\propto }{(1/i)}
well i warn sum of H.P. has no formula.....ise karne ka sirf gadha ghora hi gadha ghora tarika hai...:):P
-
UP 0 DOWN 0 0 41

41 Answers
nishant bhaiya....how to end the solution??? and harsh's reason look good!! What will be the answer in this case??
yes that is the way
harsh has done is absolutely correct...
This was the latest sms of the day ?! :)
see that we have infinitely; many clubbed terms each greater than 1/2..
So the total sum will be greater than infinity :)
That's an interesting statement: "So the total sum will be greater than infinity :)" [1]
\\1/2+1/3+1/4+1/5+1/6+1/7+1/8+1/9+1/10+1/11+.................... \\1/2+(1/3+1/4)+(1/5+1/6...+1/8)+(1/9+1/10+...1/16)+....... \\>1/2+2\times1/4+4\times1/8+8\times1/16+........ \\>\infty\times 1/2
LOL....yes i liked it too...
So the total sum will be greater than infinity :)
see the proof of the same and you will realize that you are using the same thing as the proof given here in this thread [3]
ha ha he he [4]
it is famous summation
my brother told me its solution in summer holidays of +1[3]
pleaze tell me about the SMS !!!! i had made account on targetiit 1.5-2 month ago??
go to http://www.targetiit.com
and register for the sms services!!
its free too!![1][1]
Cant think of any Gallardo...
Do you knwo of any?
What about \sum{\frac{1}{r^{1.5}}}
I dont think that helps..
because the lim sup of the limit is 1, that too it approaches from a value of less than 1...
So we cannot give any conclusion...
well , there is an another method to prove the same thing
convert the summation in form of integration
\sum_{r=1}^{\propto }{\frac{1}{r}}=\sum_{r=1}^{\propto }{\frac{1/n}{r/n}}
here put
Limit (n→∞)
and convert it to definite integration
\int_{0}^{1}{\frac{1}{x}}dx
it will shows that sum is not finite
Finally the sum made sense harsh! thanks for the summation of series way...lol.
S(n)=1+1/2+1/3+1/4+1/5+...+1/n
S(1)=1
S(2)=(2+1)/2!
S(3)=(3!+3+2!)/3!
S(4)=(4!+4x3+4x2+3!)/4!
S(5)=(5!+5x4x3+5x4x2+5x3x2+4!)/4!
The stuff in parentheses forms the following pattern:
S(5)=(5!+5!/2+5!/3+5!/4+5!/5)/5!
We can divide top and bottom by 5! and get:
S(5)=1+1/2+1/3+1/4+1/5
Oops!
That's what we started with. All I did was show that S(5)=S(5). Actually, we can go directly from the last step (just above the Oops!) to the step above that with all of the 5! in it. Just multiply top and bottom by 5!
It turns out that there is a relatively simple estimate of the sum of n terms:
S(n) is approximately ln(n)+.5772156649...
It gets closer, the larger n is. The number .5772156649... is known as Euler's constant (or the Euler-Mascheroni constant), and is represented by a small gamma.
S_{\infty }=\lim_{n\rightarrow \infty }\int_{0}^{1}{\frac{1-x^{n}}{1-x}}dx
will this help.....or not[3]
btw i dun hav any idea abt ur gadha ghora method[3].......surely hearing from u tat term first time....may be its called something else also....
GADHA GHORA method means ass-horse method:P
not that ass tho :P
any ways the process is approximation not hit and trial
lol..
was my face like that :D
Aise this is not that bad! I think this is a important sum to find! (atleast to konw ;))
okie.. try to prove this
The sum given is not finite! [1]
by comparing or showing that it is larger than another infinite series.
yea.............or drawing the graph of y=1/x......and finding area...[3][3][3]