21"since angle B = 2 angle C so, b2= c(a+c)"
show it ; (ISI entrance 2007 objective)
ABC is a an acute-angled trianlge in which LB = 2LC
and AD is the internal bisector of A which meets BC at D such that, CD = AB
prove that, LA = 72°
An interesting problem no doubt but an easy one though..!! Its from RMO 2001
-
UP 0 DOWN 0 0 9
9 Answers
36There are two ways to do this...
One of the easiest way is,
since, LB = 2LC
so, b2 = c (c + a)
as c = n so,
or, b2 = n2 + an ---- (i)
Again, by angle bisector theorem,
c/b = m/n
but, c = n
=> n2 = b x m ---- (ii)
putting, the value of n2 from eqn. (ii) in (i) we get,
b2 = bm + an
Again, a = (m + n)
so, b2 = bm + n(m + n)
or, b2 = bm + mn + n2
=> b2 - n2 = m (b + n)
=> (b + n)(b - n) = m (b + n)
=> b - n = m
=> b = (m + n)
what???
a = b
so, LA = LB
Let, LC = x so,
LB = LA = 2x
so, 2x + 2x + x = 180°
=> 5x = 180°
=> x = 36°
so, LA = 2x = 2(36°) = 72° proved..
Algeometry
2136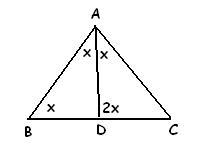
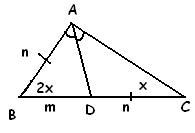
Let ABC be the triangle in which LA = 2LB
Now, we draw AD from A meeting BC at D such that it bisects A
let, LB = x (say) ,
so, LA = 2x
=> LBAD = LCAD = x (by our construction)
Also, by angle-bisector theorem
AB/AC = BD/CD
clearly, AB = c , AC = b and BC = a
so, c/b = BD/CD
=> (b + c)/b = a/CD ---- (i)
Again, Triangle ADC ~ Triangle BAC clearly,
so, AD/AB = CD/AC = AC/BC
or, AD/c = CD/b = b/a
=> CD = b2/a ---- (ii)
putting the value of CD in (i) we get
(b + c)/b = a/(b2/a)
=> a2/b2 = (b + c)/b
=> a2 = b (b + c) proved... :D
What is ISI by the way??
36There is one more way to work this question out..
>> Its by pure geometry.
21ISI is Indian Statistical Institute.......its the best place for stats and maths...........
21Can u answer why its indian statistical institute not indian institute of statistics? :D
36@Subhodip - What r u talking bout???
If u r talking bout the script... then its a self designed one of mine...
i've written some html codes for it... just for fun... !!
i've used a simple programming in JS....!!
onclick = 'alert(".....")'
:D