Paragraph for Question
When we see the bottom of a vessel filled with liquid using paraxial rays then the bottom appears to be raised by a distance where t is the real depth and is the refractive index of liquid. On the contrary when an observer inside liquid sees the outside world, the objects appear to be farther by a distance (μ - 1)t. Let us consider the following case:
The bottom of the cylindrical vessel is a plane mirror. A bird is managing to be at rest at a height h above the mirror. Liquid of refractive index μ is filled in the vessel at a constant rate such that y increases at a rate v. Answer the following questions:
Now the bird starts moving vertically downwards with speed v. Answer the following question.
Ques.
The speed of the image of bird formed in the plane mirror is
1. (μ - 1) v downwards
2. (μ - 1) v upwards
3.v downwards
4. v upwards
1Speed of the image in the mirror is asked .
answer should be 2)
V=\mu h+y \\\Rightarrow \frac{dV}{dt}=-v\mu +v=v(1-\mu )
I have taken V positive downwards. and dVdt is coming -ive.
hence the image is moving upwards.
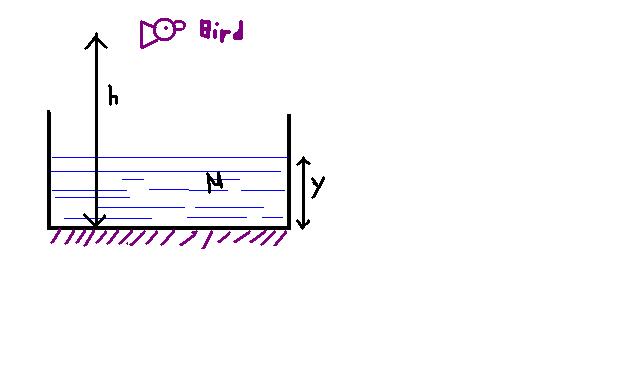
3from the bottom of the tank if seen we get ..
(h-y)/1 = h(app)/u ....[note distances are always measured frm water interface]
(h-y)u + y behind the mirror the image is formed .......
now again on the rays way back out of the water [if its the bird whcih sees its reflection].....
[(h-y)u + 2y]/u = h(app1)/1 ..
dh(app1)/dt = req. result
if are askin for the image seen by an observer inside the water .......
its just
d/dt[(h-y)u+y]
guys the distances are always measured frm interface ........
