but here they r askin the radius.........i need the soln. pls/...
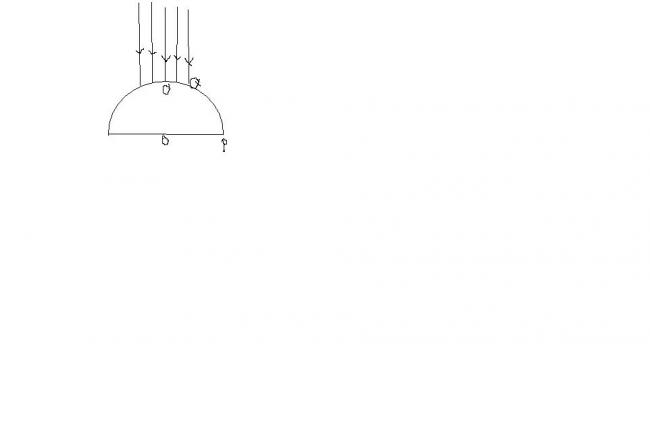
The radius of the beam of light 'r' falls on the hemispherical glass of radius 'R'(μ=4/3). Find the radius of the image formed at the base of the hemisphere.(it is kept on the table)
-
UP 0 DOWN 0 0 15

15 Answers
http://targetiit.com/iit_jee_forum/posts/y_g_2400.html
similar to this one
for this question, I think we should use pure geometry. If r is not very small.
Otherwise it will/ could giev approximation errors...
I have a more different version of the answer..
my result gives me 3/4 r when r is very small..
Is your answer dimensionally giving length?
bhaiyya my answer also gives 3r/4
and it is certainly dimensionally correct (i think u misread my result ive added a few more brackets now)
check the denominator..
is it 3r2 or 9 r2!
Our answers are a bit different.
but it gives me a feeling that you(or I) may be making only a slight mistake!
The final answer is different by a huge margin .. but all the terms and smaller expressions seem to be the same ;)
:(
checked it once again only 1 mist i found
the 3r2in the denominator
if there is still some mist :(
sir.... the answer for same Qs. with μ=√3 and radius of beam is √3r/2..
is r/√3........ u r rite... there is some good geometrical knowlege required.. but i didn't get wat it is(only key was given)
not too much sriraghav.. this is a dirty solution...
I dont have a camera right now... will try to post the solution tomorrow..