11bhaiyya what is luminous point
a beam of light incident vertically on a glass hemisphere of radius R and refractive index √2 lying with its plane side on a table. the axis of beam concides with the verticle axis passing through the centre of base of the hemisphere and the cross sectional radius is R/√2. find the point where luminous point is formed
-
UP 0 DOWN 0 0 11
11 Answers
11On the centre..........yes sri...light ray is incident along the normal.......so no deviation.
62√2/v-0=(√2-1)/R
v=R√2/(√2-1)
v=R√2(√2+1)
v=R(√2+2)
again
new u for second refraction is given by v-{R(1-1/√2)}
=R(√2+2) - {R(1-1/√2)}
= R{ (√2+2) -1 + 1/√2}
= R{ 1 + 3/√2 }
now
√2 R{ 1 + 3/√2 } = D
R{ 3+ √2 } = D from the other surface.
1new u for second refraction is given by v-{R(1-1/√2)}
ye line kaise aai
62that comes from geometry..
It is an improtant calculation..
let me show that too...
Btw is the answer correct?
62
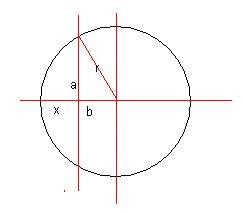
we know a is given by R/√2
so b2+a2=r2
will give b
then b+x=r
this will give x
Btw .. may be i have made some calculation mistake.. I am not very sure.. I think the method should be ok...
Or may be I am solving something else?
1KYA IS TARAH K CALCULATION BASED IIT MEIN AA SAKTE HAIN... ITS OBJECTIVE
1lekin u for second surface to
√2R(√2+2) + {R(1-1/√2)} ye hona chaiye ????????????