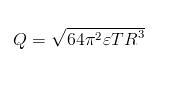SIR IS THE ANSWER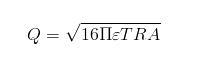
Consider a drop of conducting liquid in gravity free space. Its radius is R while the surface tension of the liquid is T. Now the drop is supplied some charge Q. For what values of Q is the drop stable.
-
UP 0 DOWN 0 5 14

14 Answers
have u doubt pllzz help after trying SIR's prob::: if a soap bubble is given a negative charge wht 'll happen to its radius (dec/inc/remains constt./first inc/then dec.)
sir ia m also getting the answer as ut10 .
stable here means that when charge is given to conducting shell the charges will repel and surface tension will hold them together . thus stable means the surface tension should be able to hold them .
possible
- √64∩2εR3T≤Q≤√64∩2εR3T
sir please verify.
consider one half of the sphere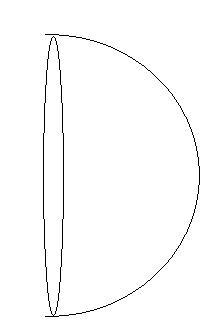
and for equilibrium we have
\frac{\sigma^2}{2\epsilon_0}*\pi r^2=2\pi r T
\sigma=\sqrt{\frac{4\epsilon_0 T}{r}}
Those result you guys have got (q \le \sqrt{64\pi^2\epsilon_0 T R^3}) is not exactly correct.
Let us see what are energy considerations when the drop breaks. Since for a given volume, the energetically favorable condition will be to have the least surface area, it will be most favorable (at least energetically) for a given drop to break only in two parts with the charge divided equally in two halves. The radius of the new drops will be then r=\dfrac{R}{\sqrt[3]{2}}. To simplify calculations (and to look at the extreme case), we imagine that the two daughter drops are far apart so as to have negligible interaction.
The initial energy of the single drop:
U_i = \dfrac{q^2}{8\pi\epsilon_0 R} + 4\pi R^2 T
The final energy of the two drops far apart:
U_f = 2\dfrac{(q/2)^2}{8\pi\epsilon_0 (R/\sqrt[3]{2})} + 2\cdot 4\pi \dfrac{R^2}{(\sqrt[3]{2})^2} T= \dfrac{2^{-2/3}q^2}{8\pi \epsilon_0 R} + 2^{1/3}\cdot 4\pi R^2 T
So the increment in energy
\Delta U = U_f -U_i
= -\dfrac{(1-2^{-2/3})q^2}{8\pi\epsilon_0 R}+(2^{1/3}-1)4\pi R^2T
The breaking-up is possible only if the final energy is less than the initial one, i.e. ΔU ≤ 0. i.e
-\dfrac{(1-2^{-2/3})q^2}{8\pi\epsilon_0 R}+(2^{1/3}-1)4\pi R^2T \le 0
This gives q\ge \sqrt{32\pi^2 TR^3\left(\dfrac{2^{1/3}-1}{1-2^{-2/3}}\right)} =q_c
For any charge q greater than this critical charge (qc), the drop could break into two parts. However, this is not spontaneous. The breaking requires a potential energy barrier to be crossed. The point is that if the force on a unit area on the drop becomes too great to be contained by the surface tension, then some pieces start to leave the drop giving way to the drop explosion. The balance of forces gives the maximum charge (beyond which the drop is definitely going to burst) qm as
\dfrac{1}{2\epsilon_0}\cdot \dfrac{q_m^2}{16\pi^2R^4}=\dfrac{2T}{R} \quad \Rightarrow q_m =\sqrt{64\pi^2\epsilon_0 TR^3}
(This is the part you guys have done)
If you compare qc and qm, we have
q_m =8\pi\sqrt{\epsilon_0 TR^3}
and
q_c\approx 4.74\pi\sqrt{\epsilon_0 TR^3}
Definitely qm > qc.
Conclusion: If the charge on the drop q > qm, the drop will spontaneously explode but if q< qc, the drop remains stable; for intermediate values of q the drop may break into one, two or more parts but slowly (not an explosive result).