hey manmay how did u start a question in thiw section . only admin can do it.
A cylinder of mass M is placed on the top of a block of mass 2M. Neglect the friction between block and the horizontal plane . But friction coefficient between cylinder and the top surface of the block is \mu . A small body of mass M travelling with a velocity of v0 hits the block horizontally. Collision is completely elastic. Find the maximum value of v0 for which the cylinder does start pure rolling before it topples from the top of the block .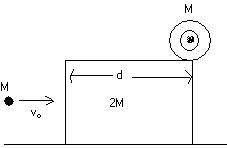
-
UP 0 DOWN 0 0 15

15 Answers
Sibal I have the rights to allow people to post questions on QOD..
THere are a lot of users here (generally old ones who have this right... )
See the past.. lots of users including Prophet sir, Kaymant sir, Abhishek priyam, Celestine and eureka, Bhargav have posted these....
ok if not the full soln then let me start the initial analysing...tell me wethr i am right or wrong...
frstly due to the inertia the cylnder will try to remain in its position whilst the block will move past...due to this sliding the friction comes into play and the ball starts rotating in anticlockwise orientation...[1]
now we have to consider the translational part...
supposing the inertia thing is correct consideration we move forward like this...
let velocity of the block initially is v....
the friction acting on it in backward direction...let friction=f
so acceleration in backward direction= f/2M
now if the cylinder remains in its own position whilst the block translates then time taken for the cylinder to fall off is time taken by the block to move forward by d distance
now, d=vt-1/2at2..
this quadratic gives us the time t...
now i have a doubt wether or not the consideraton that friction f remains equal throughout the journey period is true or not...[3]
next for the cylinder, angular acceleration α=Γ/I=frMr2=fMr=2a/r
so in the time t...found out in previous to previous post...
ω=αt=ftMr=2at/r
now the most important part....how to find out the value or v...
that is after the collision occurs..
so for totally elastic collisions, e=1
and ΔEnergy=0
so, velocity of separationvelocity of approach=1
or, v+v'=vo [+ since the mass gets reflected back...]
and 12Mvo2=12.2Mv2+12Mv'2
so that gives v
and ω is ignored in energy expression becoz ω=0 at time the small mass hits the block...
so except for the numerical part i thnk theoritically the problem is done...[1][1][1]...yay!!
solving, v=-23vo
sorry i considered solid cylinder in this problem instead of hollow one...
so wrote I=12Mr2...
so i ll have to edit evrythng...will do it in few mins....please bear till then....
maximum vo=9ft4M
again maximum case achieved when friction is limiting...i.e μMg for this case...
thus
max vo=94μgt
now i have a problem...i am getting two vlues of t...since it is obtained from a quadratic...
now to maximize vo the value with (+) will give max but when the time wid (-) is achieved the cylinder falls off.....so i thnk we shud take that value only!!!
t=2v±√4v2-8ad2a=v±√v2-2ada...[1][1]
and apologies......the actual soln is not so FAT as it eems...it is slim...but as at that time i din have pen and paper so i had posted every single thing that came to mind here!!!!
points to be debated...
1) does the cylinder remain in the starting position throughout the journey till it falls off?
2) does friction remain unaltered throughout the journey?
3) which time to be used? the one wid (+) or the one wid (-)?
i hope that so far the forum was not active in this thread but now the forum will get active in this thread!!...(i really hope so!!)