12-03-09 Circumradius of a triangle

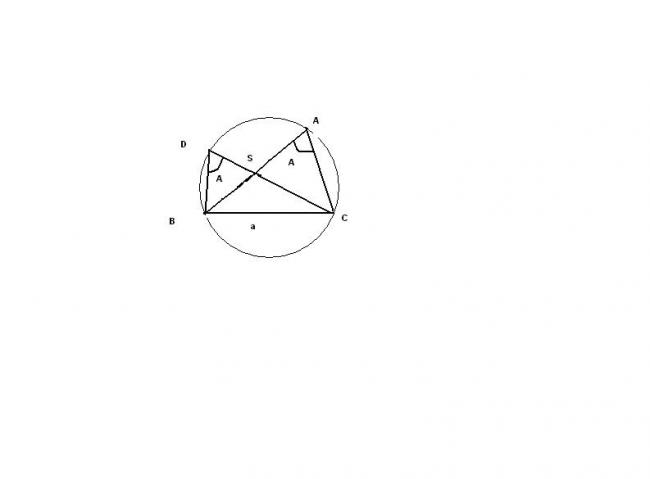
Prove that the circum radius of a triangle is given by

R = abc/4Î”

where Î” is the area fo the triangle
and a,b,c are the sides

5 Answers

we know that are of a triangle = 1/2 AB X DC
=1/2 c (ACsinA)
=1/2bcsinA
= bc/2 x a/2R ( since a/sinA =2R)
= abc/4R

refer the figure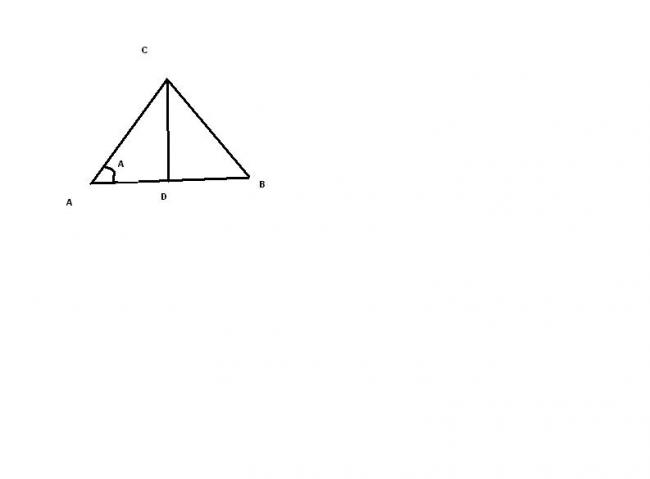

This was good.. But I want you to prove this too... I know it is easy but just for the sake of it

since a/sinA =2R

Basically I wanted the proof without any assumptions :)

if S is the center of the circumcircle and R the circumradius then in triangle BDC , rightangled at B with angle BDC= angle BAC =A

sinA= sin angle BDC= BC/DC =a/2R

hence a/sinA =2R

Awesome work amit :)

thanks bhaiya

√ √ || {} [] () → ~ ^ x x x → → ln log lg lim lim cos sin tan cot arcsin arccos arctan

∫ ∫ ∫ ∫ ∫ ∬ ∬ ∬ ∬ ∬ ∭ ∭ ∭ ∭ ∭ ⨌ ⨌ ⨌ ⨌ ⨌

∑ ∑ ∑ ∑ ∑ ∮ ∮ ∮ ∮ ∮ ∏ ∏ ∏ ∏ ∏ ∐ ∐ ∐ ∐ ∐

+ - × ÷ ± ∓ = ∪ ∩ ≠ ∼ ≈ ∅ ∀ ∃ ∈ ∋ ∝ ≤ ≥ ≃ ≅ ≡ < > ≪ ≫ ⊂ ∉ ⊃ ⊆ ⊇ ⇒ ⇐ ⇔ ⇒ ⇐ ⇔ ⇑ ⇓ ⇕ → ← ↔ → ← ↔ ↑ ↓ ↕ ↖ ↗ ↘ ↙ ↪ ↩ ⇀ ↼ ⇁ ↽

° ∂ ∞ α β γ δ θ λ μ ν ξ π ρ σ φ ω ε ƒ κ τ υ Γ Δ Λ Σ Π Ω