12-05-10 Rotation

JEE Mains Discussion Forum › Question Of the Day questions › 12-05-10 Rotation

A cylinder of mass M and radius R is rotated in a uniform V groove with constant angular velocity Ï‰.
The coefficient of friction between cylinder and each surfave is Î¼.
What torque must be applied to the cylinder to keep it rotating ?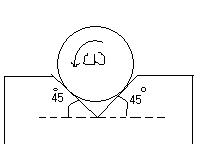

#Miscellaneous #Question Of the Day

UP 0 DOWN 0 0 4
Post on FacebookPost anonymously?

4 Answers

student ·2010-05-12 00:46:11

hint:(friction is kinetic)

UP 0 DOWN 0
Post on FacebookPost anonymously?

Bicchuram Aveek ·2010-05-12 01:10:11

Is the answer

âˆš2 Î¼1 + Î¼² MgR ???

not so sure as it does not involve Ï‰ .

UP 0 DOWN 0
Post on FacebookPost anonymously?

Subhomoy Bakshi ·2010-05-12 04:36:47

i am getting simply âˆš2Î¼MgR...wer from are u getting such an answer?

UP 0 DOWN 0
Post on FacebookPost anonymously?

Subhomoy Bakshi ·2010-05-12 04:49:26

my solution..

normal reaction's horizontal components balance each other
vertical component balance weight..

2Ncos 45Â°=Mg

so, N=1âˆš2Mg

so, f=kinetic friction=Î¼N=1âˆš2Î¼Mg

torque by individual friction=f.R=1âˆš2Î¼MgR

so net torque due to 2 frictions=âˆš2Î¼MgR

so torque required to be applied in order to keep uniform rotation=âˆš2Î¼MgR

show wer i am wrong and also post ur solution aveek..a.k.a. bruce lee LOL

UP 0 DOWN 0
Post on FacebookPost anonymously?

Your Answer

Basic Integral Calculus Operators Symbols Matrix Cases

√ √ || {} [] () → ~ ^ x x x → → ln log lg lim lim cos sin tan cot arcsin arccos arctan

∫ ∫ ∫ ∫ ∫ ∬ ∬ ∬ ∬ ∬ ∭ ∭ ∭ ∭ ∭ ⨌ ⨌ ⨌ ⨌ ⨌

∑ ∑ ∑ ∑ ∑ ∮ ∮ ∮ ∮ ∮ ∏ ∏ ∏ ∏ ∏ ∐ ∐ ∐ ∐ ∐

+ - × ÷ ± ∓ = ∪ ∩ ≠ ∼ ≈ ∅ ∀ ∃ ∈ ∋ ∝ ≤ ≥ ≃ ≅ ≡ < > ≪ ≫ ⊂ ∉ ⊃ ⊆ ⊇ ⇒ ⇐ ⇔ ⇒ ⇐ ⇔ ⇑ ⇓ ⇕ → ← ↔ → ← ↔ ↑ ↓ ↕ ↖ ↗ ↘ ↙ ↪ ↩ ⇀ ↼ ⇁ ↽

° ∂ ∞ α β γ δ θ λ μ ν ξ π ρ σ φ ω ε ƒ κ τ υ Γ Δ Λ Σ Π Ω

Close [X]

12-05-10 Rotation

4 Answers

Your Answer

Add Image

Similar Questions