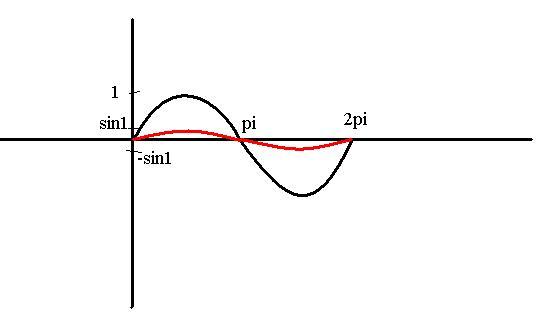
Is it 3?
What is the number of points of intersection of sin x and sin (sin x) in the interval [0, 2 pi]
-
UP 0 DOWN 0 1 13

13 Answers
sin(sinx)=sinx
=>sinx=nπ+(-1)nx
n=0 => sinx=x =>One soln( x=0)
n=1 => sinx=Ï€-x =>One soln(x=Ï€)
n=2 => sinx=2Ï€+x =>no soln
*Edit*
n=-2 =>sinx=-2Ï€+x =>x=2Ï€ is a soln
So 3 soln in x ε [0,2π]
*Edit*
nishant sir wont give such an easy question...i think there is something else to it also....
@eure 2pi is also a solution
@eure yaar 3 soln toh already evident . i.e at x=0,pie,2pie.......i thnk there is no other soln other then these.........
yaah ..that i know....but why not coming htrough my approach
spot the mistake
sina=sinb implies a=npi+(-1)^n b only when a belongs to [-pi/2,pi/2]
[299]
i found a cool smiley..yippeeee
"nishant sir wont give such an easy question...i think there is something else to it also...."
LOl.. :D
No guys I give easy questions most of the time I think [3]
All I wanted to see is a graphical approach and deepak and the rest of you have done it perfectly :)
arey sir i thought that as u gave it.....there may be some unexpected twist in it....
[299]
[4][4][4]
[4][4][4][4]
[4][4][4][4][4]
[4][4][4][4][4][4]