concentric circles with radii between 1(k+1/k)2 n 2(k+1/k)2 units with center at (0.-2(k+1/k)).. ??
This is another good one about complex numbers. I am not trying to get a solution. I am sure many of you can.
I got this question from a user(Integrations) here. (I modified that one slightly!)
I want to stress the importance geometry can play in solving questions of Complex numbers. And why the importance of understanding Argand plane's equivalence with the XY plane of coordinate Geometry!
Find the locus of z such that
|z.k + 2i| > √2 for all real values of k
and that z is in the 4th quadrant.
Note: I have changed the language of the question to take away all the complexities.. so that you get a much simpler thought process :) I hope this hleps.
-
UP 0 DOWN 0 0 51

51 Answers
is z a semi-circular ring with inner radius 1(k+1/k)2 n outer radius 2(k+1/k)2? (since z is in 4th quadrant )
no maddy it is not a circle..
see the thing given is that k could be any real number..
i dont know appolinious circle.. but the final solution has nothing much to with circles ;)
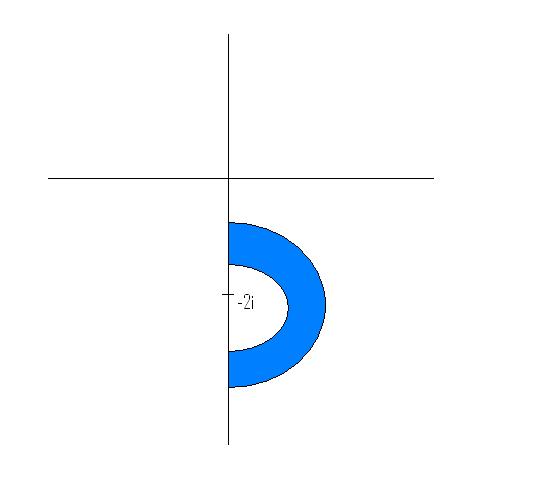
concentric circles with radii between 1 n 2 units with center at (0.-2).. ??
but it is given for all real values of k!!
where is value of k that u will take!!
it is not
1<|z.k/(k+1)| < 2
no maddie...
see the problem is that k is not a fixed number.
Example:
for a fixed k, kz gives another complex number
for all real values of k, kz will give infinitely many points (which turn out to be ....)
no..
Celestine.. i think all of u have got confused.
there are 2 things.. both have seperate answers
1) find all x such that x>k for a fixed k
2) find x such that x>k for all real values of k.
all of u are answering using k as in part 1!
i want k as part 2... read the question carefully!
well maddie this is not the correct thing..
well tried..
see the problem is that the center of the circle changes with every k
so the center is dynamic.
Wait i will make this question much simpler!!!
Let me rechange the question.. bcos it seems that this has become too tough!
excluing portion btw
x2+(y+1)2= 1 and 1/2
Zk/K+1 lies btw x2+y+22 = 1 and 2
Zk/k+1 is point dividing 0 and Z in ratio k:1
k=-1 gives z as midpt of kz/z+1 which is impossible
so all other sol are possible were z vector cuts the circles its possible upto tangent at outer circle givin x=-y
so its lower half of 4 quad excluding wat i wrote above
celestine but the question has changed in that time! :(
sorry to shuffle the queston around!
But i was having a feeling that no one is understanding the essense..
so i removed a few things to make it simpler.
and now it has a much more elegant proof and will explain much better (with simplicity) what i wanted to as well :)