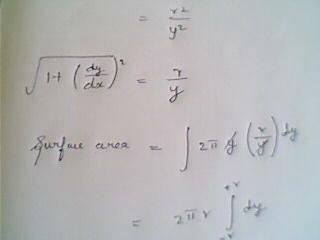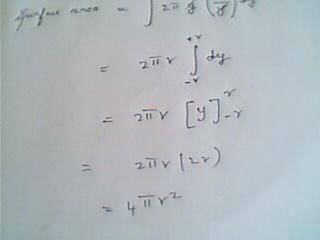1Mmm... how cld i explain u!!!!!!!!!!
k.. byah.. wait...
Prove that the surface area of the sphere is indeed what we read in our childhood as
4Ï€R2
-
UP 0 DOWN 0 0 24
24 Answers
9jus the standard one passing thru centre ( u need to assume )
9for volume its integration of 4pir2dr
For MOI its integration M/V(4pir2 dr)X r2 =M/V(4pir4dr)
proceeding ull get
3@eurekas question
ok ill do MI of sphere ...[method...:P]
u can visualise it as its chopped up into a number of discs ...[just like bfre]
now lets take a disc at dist. y frm center of sphere and its thickness be dy ...
its radius(r) = √R2 - y2 [ frm ricky pointingpythagoreas theorm [9]]
MI wrt center
1/2Ï pi r2 dy + Ï pi r2 dy y2
integrate the abve expression frm -R to +R in order to get the answer!!!!!!!!
1dats rit..
k.. then.. no more confusions...
but i m sure wit dat proof in #3...
dats was actually one of d proofs in ma 11th book...
but neways its k........
62hmm.. but then what is length and diameter?
Even I remember having done something like that.. but i guess that now you know integration and stuff.. so there is no need to get lost in such old formulas :)
1remember dat i read it in lower standards byah..........
not very sure of it.. but 95% sure... pls don scold.....;-(
24If Nishant sir permits....
Surface area was easy actually.....Can u derive Volume and moment of inertia of sphere???????????
it will be a bit tricky.[1][1]
1isnt it simple???
surface area = lenth * diameter..
length i mean d perimeter..
so S.A=2pir*d
=2pir*(2r)
=4pir2
3sky vertical horizontal....all the same ... only ur perception,,,,
1the surface area can be written as
\int_{0}^{\pi }{2\pi Rsin\theta .Rd\theta }
and we know that the integral of sin from 0 to π is 2 units
DONE!!
is it too subtle to need an explanation ?
3takin vertical discs is easier actually
∫2pi(√R^2 - y^2)dy
within limits -R to +R ..............................
y is the distance of the center of the dic frm the center of the sphere ........
and we get the radius of the small discs using pythagoreas theorm [3]
1considering d sphere to be intercepted between two parallel planes at a distance -r and +r frm d centre.. .....
62are you taking vertical discs?
I did not understand what circels you are taking?
1byah.. dis proof is easy or suggest a better n easyone....
