1I found something over here though,
http://www.mathsisfun.com/geometry/ellipse-perimeter.html
http://www.efunda.com/math/areas/EllipseGen.cfm
[1] and I thought only i was finding it tough :P
An ellipsoid is given by
x2/a2+y2/b2+z2/c2=1
find the volume of it
-
UP 0 DOWN 0 0 20
20 Answers
21I m sure this one can be done using Rotation abt an axis.....
Due to the third dim c≠b it gets a lil triccky ........
I found a crude way though using approximation
I found the Vol. of ellipsoids given by
x2/a2 + y2/b2 + z2/b2 = 1
x2/a2 + y2/a2 + z2/c2 = 1
x2/c2 + y2/b2 + z2/c2 = 1
As :
4Î ab2/3
4Î ca2/3
4Î bc2/3
NOW taking Geometric mean of the above three results obtained by approximating one of the dimensions...
we get Vol = 3√4Î ab2/3 * 4Î ca2/3 * 4Î bc2/3
Vol = 4Î abc/3
11Yes Celestine I not only thought but worked out a very ugly and big expression for perimeter using Rdθ
so surface area of ellipsoid bcomes even more complicated , any help here ?
24Did by this method six months back when i was learning definite integral
other shorter methods may be there
1no that is why i asked
had i known the perimeter of ellipse i would have found out the surface area of the ellipsoid easily
im getting a very ugly integral as expression for perimeter of ellipse !
62philip you can find the perimeter easily..
you have to integrate elementary areas :)
Think of how you fidn the perimeter of ellipse
Something similar here?
21No u dint....
Ur answer is perfectly fine, but i was trying to do by Rotation of Axis
21Wait...... I'm thinkin of a better methd using addition and subtraction of Volumes rather than this approxiamtion technique......... [12] [12]
1area of ellipse vol of ellipsoid is easy
but can anyone tell me how to work out perimeter of ellipse
OR
surface area of ellipsoid
though the perimeter of the ellipse may be wrongly guessed as π(a+b)
how can one guess surface of ellipsoid
is it 4Ï€(abc)2/3 :D :D
and btw what about the moment of inertia of the ellipsoid !
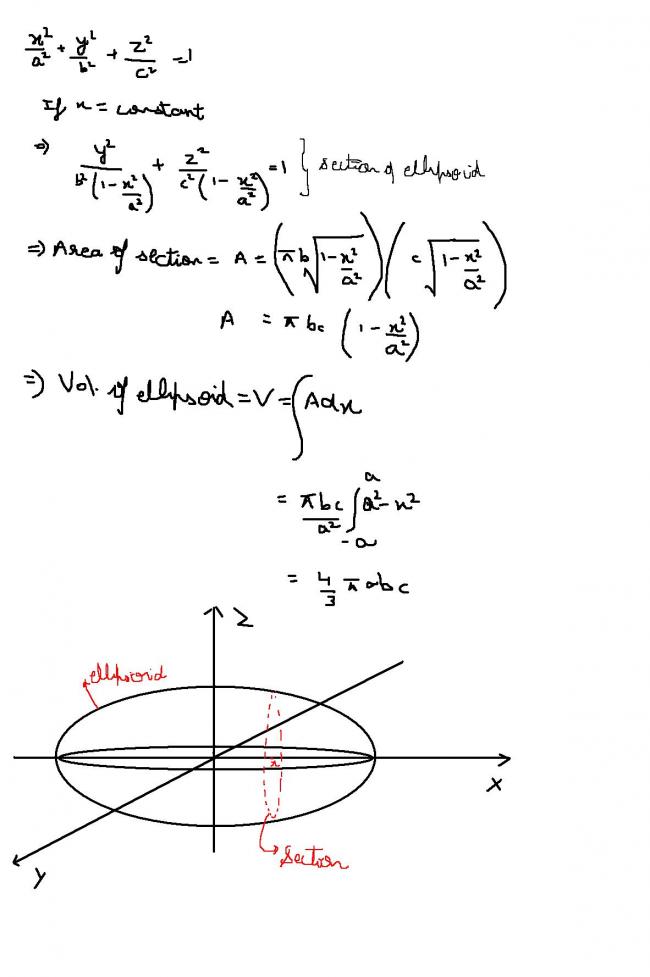
1All we need to know is that the area of an ellipse is πab
then taking element as a thin ellipse
we can write the volume as :-
\int_{-a}^{a}{\pi \left(\sqrt{c^{2}-\frac{x^{2}c^{2}}{a^{2}}} \right).\left(\sqrt{b^{2}-\frac{x^{2}b^{2}}{a^{2}}}} \right)dx
this should do
1@ Tapan
"This I think will be done by rotation of 2-D figure abt an axis ........"
no it cant be done that way !
ok here goes .....
62yup it is not very tough ....
Dont knwo why not too many ppl are interested :(
21This I think will be done by rotation of 2-D figure abt an axis ........
Definite Integration se ho jana chahiye .....
Cmon Juniors!!
24ok..
i will wait for others to do that...
if they dont then i will post tonite..