then i got the same old answer
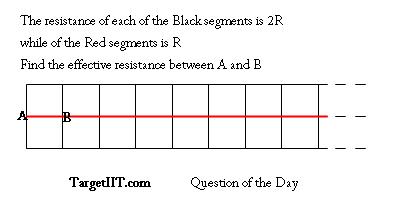
Find the effective Resistance between A and B in the given circuit!
-
UP 0 DOWN 0 0 22

22 Answers
Yes i did.. so there was a small trick.. find R' using the method first..
and then again use it in the circuti to find the equivalent resistance across AB! :)
R'= (R+R'+2R)*2R
(R+R'+2R)+2R
above is wrong..
i have edited suitably below
R'= (R+R'+R)*R
(R+R'+R)+R
dear i am sorry i catn get ur mind..
can u mail me the image at nishantsah at targetiit.com
i will check the image..
sorry for troubling u
I am unable to get the picture .but let me try explaining .let R effective be R' 2R ,2R in series with R'(assuming the infinite sequence as R')this in parallel with R.that gave me (2√2-2)*R
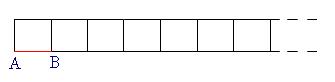
so we are reduced to this circuit.. where each of the small part has a resistance of 1 ohm!
so the new question now boils down to finding the resistance across AB of this circuit!
This is again not very tough.
we know the resistance of the points between B and the point above B.
that is a standard question which u must have seen so many so many times :)
basically u replace that here. by the effective resistance...
so u are reduced the square loop... with 4 resistances only.. i hope this question helped u guys :)
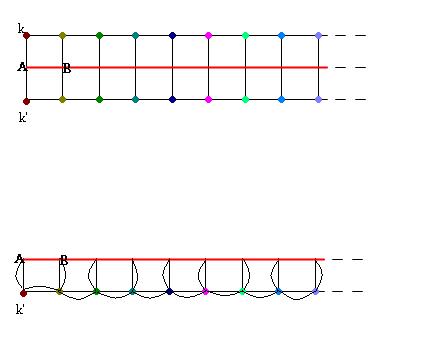
In the above figure, .. there is a symmetry about the red line.. or about AB.. so what happens is that the same colored points on either side of the red line are equipotential.. if we apply a potential across AB..
so for this circuit, if we joined these points together, it will not change the equivalent resistance.
on joining them, we will get the lower equivalent of the above figure..
where each black line is of resistance 2ohms.. and the red line of 1 ohm...
each node has 2 wires between them .. each are in paralllel..
so we can reduce it to the figure below:
continued in the next post:.....
dude.. let me check 1 sec.. i have an anser in another form.. but may be u are right :)

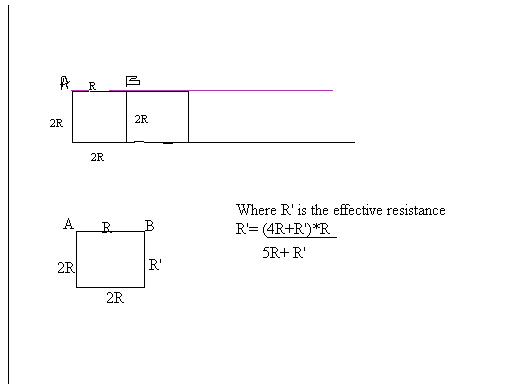
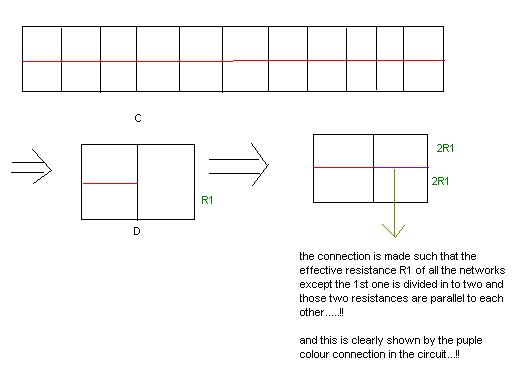 hey is equivalent cirrcuit diagram like this........
hey is equivalent cirrcuit diagram like this........