Question 1)
p(x)= 51x101 - 2323 x100 - 45x +1035
Prove that atleast one root lies between
(451/100, 46)
Question 2)
for -1≤p≤1, show that 4x3-3x-p=0 has a unique root in the interval [1/2, 1] and identify it.
Question 3)
P(1)=0 and dP(x)/dx >P(x) for all x≥1, prove P(x)>0 for all x>1
Question 4)
a+b=4, where a<2 and let g(x) be a differentiable function. If dg/dx>0 for allx, prove that \int_{0}^{a}{g(x)dx}+\int_{0}^{b}{g(x)dx} increases as (b-a) increases
Question 5)
let f(x), x≥0F(x)=\int_{0}^{x}{f(t)dt}, x≥0. If for some c>0, f(x)≤cF(x) for all x≥0, show that f(x)=0 for all x≥0
PS: Some of these are very very tough. Dont panic if you cant solve them.
21Question 1)
As the functn is cont. p(a).p(b)<0 implies a root exists b/w (a,b)
as we can c p(46)>0 and and p(451/100)<0
Ther4 atleast 1 root exists b/w them
1p(x)= 51x101 - 2323 x100 - 45x +1035
Prove that atleast one root lies between
(451/100, 46)
p(451/100) = 51*45*451/100 - 2323*45 - 45*451/100 + 1035
= 50*45*451/100 - 2323*45 + 1035
using approximation and calculating u can see that this quantity is -ve
whereas
p(46) = 51*46*46100 - 2323*46 - 45*46100 + 1035
= this quantity is +ve
so thereexists a root in between
1oho .. just when i posted the page refreshed and i saw tapan had already posted the soln.... ... [1]
21USING the same techniQ as in Q1
LET p = sinθ to make life better.......
f(1) = 1-sinθ ............ f(1)>0
f(1/2) = -1 - sinθ............ f(1/2) < 0
so der exists atleast 1 root in [.5,1]
NOW TO CHK for its Uniquejess n IDENTITY........
LET THE ROOT BE sinα as it lies b/w [0.5,1]
then we have
4sin3α - 3sinα = sinθ
sin(3α) = sinθ
1/3(sin-1p) = α.............. as p = sinθ
sin(1/3(sin-1p) ) = ROOT
I m yet to prove that this root is unique in [.5,1] I know, dat I'll do soon
21YEAH!!!!!
its uniQue also coz :
[COntradiction methd]
let ther b 2 roots in da range [.5,1]
let them be sinα and sinβ
THEN BOTH SATISFY :
4sin3α - 3sinα = sinθ
4sin3β - 3sinβ = sinθ
and hence both also satisfy
sin3α = sinθ = sin3β
FOR THIS to happen either α == β
OR α ± 2Π= β
BUT 2Î >6 and hence these values differ by atleast 6units which is >> (1-0.5)
HENCE HO GAYA NAAA......
[1]
1ok for question (2)
f'(x) = 12x2-3 > 0 for (1/2 , 12321564564) ;) i meant ∞ [but =0 at 1/2 :)]
f(1) = 1 - p so f(1) >= 0
f(1/2) = -1 - p f(1/2) <=0
we note both can't be =0 at the same time........
hence we have one unique root in [1/2, 1]
( i hope its correct) [23]
as for identifying it [12]
now i noticed that tapan has already done that :)
14 th
g(x) is an increasing function .. given
now i am talking in terms of f(x) .. which we get after integration of g(x) : assumed
f(a) - f(0) + f(b) - f(0)
= f(a) - f(0) + f(4 - a) - f(0)
= f(a) + f(4 - a) + c .. 1
b - a = 4 - 2a .. incresing this means decreasing a
now let a be decreased by h (+ ve)
expr . = f(a - h) + f(4 - a + h) + c ... 2
for this expression to be more than the previous expression
eq. 2 - eq . 1 > 0
f(a - h) + f(4 - a + h) + c - (f(a) + f(4 - a) + c) > 0
=( f(4 - a + h) - f(4 - a) ) - ( f(a) - f(a - h) )> 0
1
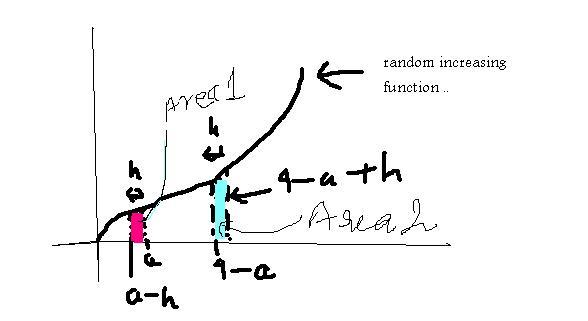
now refer the graph of an increasing function :
on decreasing a .. by increasing the value oh h the difference between area 1 ( f(a) - f(a - h)) and area 2 (f(4 - a + h) - f(4 - a))
increases ... because the area 2 increases at a rate more than area 1 ... reason u can make it out .. integration is dealt in terms of area ..
integration of g from s to d = f(d) - f(s) = area between d and s ...
21Ankit : ITs not this lengthyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyy sum bro,
HINT :
Remember "Newton dada woh Leibnitz wale"
uske liye condition kya hai : limits of integration must be VARIABLES not constants, try to introduce VARIABLES INSTEAD OF A AND B, UR SUM IS DUN
SOLUTION : (warniong : dont readahead unless u give up )
let A = 2-t; B = 2 + t
ab easily apply leibnitz
115
using leibnitz F'(x)=f(x)
using the given condition F'(x)≤cF(x)
integrating F(x)≤kecx
i cant proceed further help!
11bhaiya help [94]
that question is coming to kill me!
help!
[3](old smiley :P)
1bhaiyya for question 5 i think it must be mentioned that f(x) is non negative
1you have written x>=0 twice
i think second time it should be f(x)>=0
then
we get F'(x)=f(x) and hence from the inequality
F(x)<=F(0)*ecx
further as F(0)=0∫0f(t)dt=0
hence F(x)<=0
and from the equation f(x)<=cF(x)<=0
hence f(x)<=0 but mentioned in problem f(x)>=0
hence f(x)=0
