334) 2n+1-cosγ
2n+0∫γsinxdx
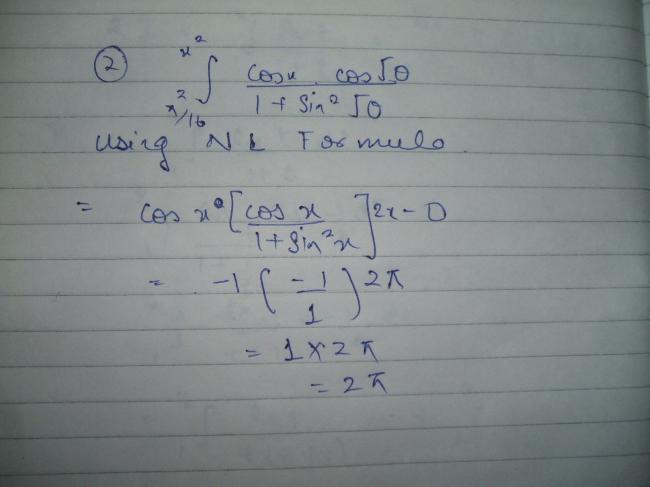
You might say why the QOD has become 5 questions a day!
but its JEE season and we have to change ourselves in a similar way ;)
Solve these: (Again a few of these are tough!)
1) for x>0, let f(x)=\int_{1}^{x}{\frac{ln t}{1+t} dt}. Find the function f(x)+f(1/x) and show that f(e)+f(1/e)=1/2
2) if y(x)=\int_{\pi^2/16}^{x^2}{\frac{\cos x. \cos \sqrt{\theta}}{1+sin^2\sqrt{\theta}} d\theta}. Find dy/dx at x=pi
3) Determine the value of \int_{-\pi}^{\pi}{\frac{2x(1+\sin x)}{1+\cos^2x}dx}
4) Evaluate \int_{0}^{n\pi+\gamma }{|\sin x|dx}.
Where n is a +ve integer and 0\leq \gamma \leq \pi
5) \int_{-\pi/3}^{\pi/3}{\frac{\pi+4x^3}{2-\cos\left(|x|+\pi/3 \right)}}dx
-
UP 0 DOWN 0 0 7
7 Answers
11 reduces to 1∫t(lnt/t)dt
2 already done earlier let others post
3- first x=-x and add then =20∫ππsinxdx/(1+cos2x)(As f(x)=f(-x)) further x=π-x and add and then put cosx=t
4-priyam answered
5-x by -x then add then as f(x)=f(-x)=20∫π/3.. after that modulus can be removed and break cos(a+b) expresss in tanx/2 form
33Q.1
f(x)=1∫xlntdt/(1+t)
1/p=t
-1/p2dp=dt
f(x)=1∫1/x-lnp(-dp/p2)/(1+1/p)
=1∫1/xlnp(dp)/p(p+1)
f(x)+f(1/x)=1∫1/xlnp/p(p+1)+lnp/(p+1)
=1∫1/xlnpdp/p
(lnz)2/2]1 1/x
=(lnx)2/2
put x=e
f(e)+f(1/e)=(lne)2/2=1/2
Proved...