66No one?
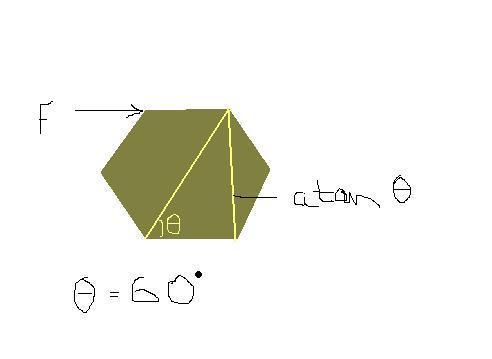
The diagram below shows the section of the pencil...
Assume that for the pencil, shape is a regular hexagon, the wooden part is massless compared to the lead inside.. so that there is only mass at the center.
The pencil is rolling on the floor. find the minimum coefficient of friction needed for the pencil to not slip after falling down from one vertex to the other...
Assumption : the limiting value of friction acts during collision/ hitting the floor....
-
UP 0 DOWN 0 2 10
10 Answers
62karna.. here the question is that on falling down on the other vertex, there should be no slipping..
I think you have taken it at that same point!
1I got the answer to be 0.28
But I have made an assumption(I don't know if it is correct).
1My assumption is that i took the pencil initially at rest...
A force of F is applied horizontally.
For body to topple,
F.a tanθ>mga2
→F≥0.28mg
For μ<0.28 the body will translate.
For μ>0.28 the body will topple.
1considering the general case of the pencil with a regular N-gon cross-section, with moment of inertia I0 about the edges and Ic about the centre.
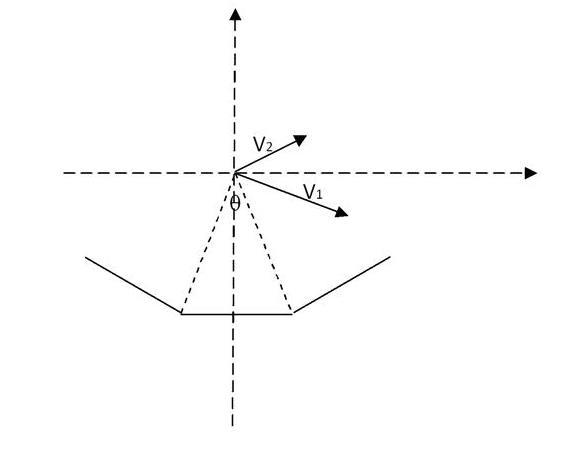
conserving angular momentum about the edge on which the pencil is falling; we get -
mv_1cos\theta l^2+I_cv_1=I_0v_2
v1 and v2 are the initial and final velocities of the CoM.l is the distance of the centre from any of the edges.
now we use (fdt) ≤ μ(Ndt) to get - [we know the quantities in parenthesis]
\mu \geq cot\frac{\theta }{2}\left[\frac{1-\frac{ml^2cos\theta+I_c}{I_0}}{1+\frac{ml^2cos\theta+I_c}{I_0}} \right]
in the current problem I0=ml2 and Ic=0 so
the expression reduces to :
\mu \geq tan\frac{\theta }{2} \ \, \; \; now\ for\ a\ regular\ N-gon;\ \theta =2\pi /N \\\Rightarrow \boxed{\mu _{min}=tan\frac{\pi }{N}}
we note as N→∞ μmin→0
Assumption : the impulse of the normal force acts at the falling edge.
One case can be when the pencil just stops after hitting the vertex, but I don't think the question is asking about that ?
1But don't you think that μmin should be less than μ required to start toppling??