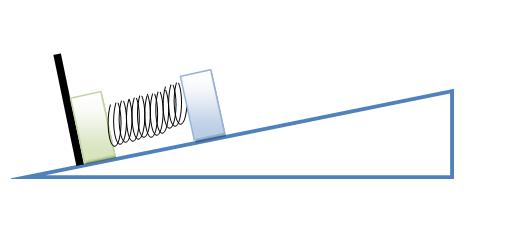
Question : What should be the minimum (total) compression in the spring so that the green block leaves contact....
Given:
The black wall is rigid
Coefficient of friciton between the floor and the masses is μ
Spring constant is k
The green mass is m while Blue mass is M
Incline below is fixed...
angle of inclination is theta
PS:
1) This is the same problem as the burning of the cloth one from Irodov ... only a few things have changed
2) I know that the spring sucks.. but that is the best i could manage while drawing it :P
62what you have found is elongation..
what is the question says is that you need to compress it so much that finally when the blue block recoils, it recoils so much that it pulls the green block along with itself..
1yeah i was feeling it was a touch odd... what a foolish one to make
I have made the edits above.... now please check
sorry for the trouble btw , the problem was I did this " on air " :D and that also in the afternoon when I am at my laziest best
and yes if there is still a mistake then u must abandon all hope that i will be able to arrive at the answer
62There is still a smalll mistake which i din pick up on the first look..
The work energy equation you have used... (-ve sign)!!
U:sing all this, compile the final answer?
1Haha [9]
I was sleeping
The first is the same as
2F=kx-ky
kx=(2M+m)g(sin\theta +\mu cos\theta)
62PHilip
look at the first equation more carefully...
It is nothign more than a linear equation :D :P
62awesome..
but it is not as difficult as it seems..
go ahead and complete the thing :)
24isnt thsi ques same as a ques asked a few days back in which everyhting was same except that blocks were on horz plane ??
1Let the required compression be 'x' :-
\frac{1}{2}kx^{2}=\frac{1}{2}ky^{2}+F(x+y)
where\;\: F=Mg\, sin\theta +\mu Mg\, cos\theta
such\; that\;\Rightarrow k.y=mgsin\theta +\mu mgcos\theta
Perhaps this is a bit too complex for the answer [7]
edit : corrected work energy eqn
11Then.........
Sir could u tell me the green block has to leave contact with wat?
62no virang i am afraid not...
You have not understood the problem correctly..
11Sir wat is the angle of inclination?
Or
Is this a equilibrium position?
1how can d green block loose contact??....i think it shuld hav been d blue block which leaves contact....
