262could u plz support ur question with a diagram ??
A cylindrical tub contains water.
We are only considering one axial plane of the cylinder (one that passes through the axis)
The cylinder is now rotated about it's axis with constant angular velocity.
Write the equation of the upper boundary of the axial plane.
Consider the point where this upper boundary meets the axis of the cylinder as the origin!
[1]
-
UP 0 DOWN 0 0 8
8 Answers
1
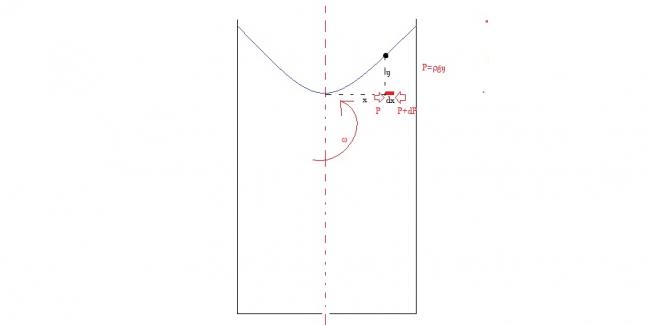\texttt{By FBD of the element dx,Balancing forces in x-direction} \\ \mathrm{dP}=\rho\omega^2\mathrm{x}\mathrm{dx}\cdots \left(1 \right) \\ \texttt{By Balancing forces in y-direction } \\ \mathrm{dP}=\rho\mathrm{g}\mathrm{dy} \cdots \left(2 \right)\\ \texttt{From equation 1 and 2} \\ \omega^2\mathrm{x}\mathrm{dx}=\mathrm{g}\mathrm{dy}\\ \texttt{By integration,we get} \\ \boxed{y=\frac{\omega^2}{2g}x^2}
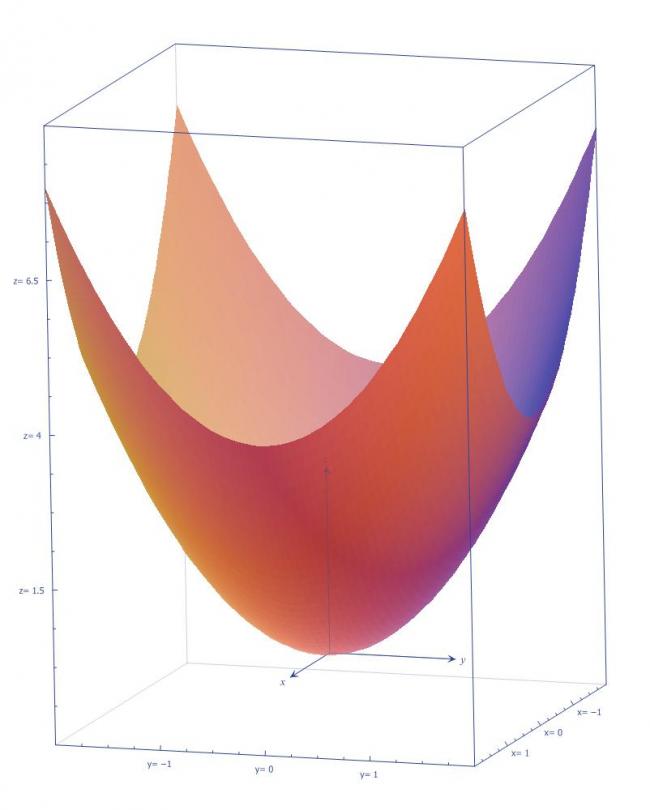
1A 3-D equation of upper surface would be
z=ω22g(x2+y2)
But in this case ,I have taken the cylinder's length oriented along z-direction
