A simple one
What is the minimum velocity you have to hit a charge q at a distance D from the center of a ring radius R and charge Q towards it along the central axis so that it stops at the center of it?
Clarification: The ring is fixed
1distance of closest approach.....(1) momentum conservation (2) energy conservation !
11The chage will be attracted towards the centre C of the ring. At C the net force is zero, and the charge has some K.E and due to inertia, it crosses C, but on the other side, it is further directed towards C.
(1/2) mv2 = U i - U f
= Up - U c [Where C is the centre and point P is from where the charge is being hit]
=q(Vp - Vc) ............................(1)
Vp = KQ/√D2+R2
Vc=KQ/R
So putting in eqn (1)
using cons of energy,
v = [(2qQk/m) [1/√D2+R2 - 1/R] 1/2
1
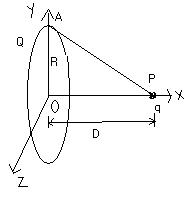
total energy at P = Ep = K.E. due to motion + P.E. Due to charge Q on ring
= 12mv2 + kQq(AP)
= 12mv2 + kQq√D2+R2
total energy at O = Eo = P.E. due to charge Q on the ring
= kQqR
now by law of conservation of energy we have Ep = Eo
→ 12mv2 + kQq√D2+R2 = kQqR
\Rightarrow v = \left( \frac{2kQq}{m}\left(\frac{1}{R}-\frac{1}{\sqrt{R^{2}+D^{2}}} \right)\right)^{1/2}
where k = \frac{1}{4\pi \epsilon _{0}}
i hope i'm rite !!
