velocity of the cylinder cant exceed the V0
A cylinder can move without friction along a straight wire parallel to its axis of symmetry, as shown.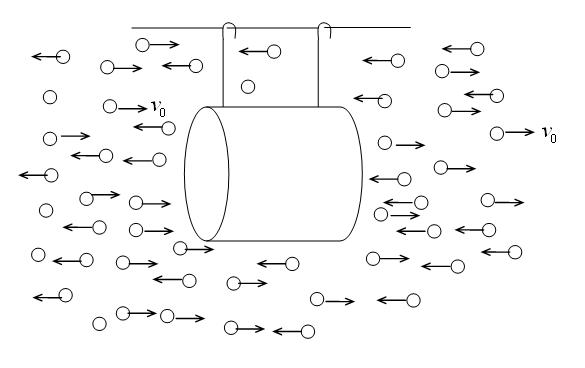
Tiny particles moving horizontally at speed v_0 bombard the body from both left and right. Collisions with the right face of the cylinder are perfectly elastic while those with the left are perfectly inelastic, though the particles do not stick to the cylinder after the collision. What is the speed of the cylinder
(i) after a long time, and
(ii) after a very long time?
-
UP 0 DOWN 0 5 28

28 Answers
perpetual mobile machine of the second kind which is against the second law of thermodynamics.
sir can u explain what this line means ???icoulndt get them
ii) After a very long time....
We can think of the small particles as the molecules of a gas at a certain temperature. If the cylinder continued to move uniformly even after a long time, it would imply a perpetual mobile machine of the second kind which is against the second law of thermodynamics.
The trouble is that we neglected the heat produced due to the inelastic collision on the left side. The cylinder heats up as it absorbs energy from the inelastic collisions. If this heat were continuously removed then the uniform motion would be possible. If the heat is not removed (as is the case in the problem) the molecules forming the side of the warm body vibrate at the average speed corresponding to its temperature, and the particles rebound from it, sometimes at a greater speed, and sometimes with lower speed than they would from a colder body. The result is that finally the cylinder cannot absorb any more heat from the gas at either end (or it would warm up further).
Averaged over time, the collisions are perfectly elastic on both ends and the impulsive forces are equal. Thus after a very long time, when thermal equilibrium has been attained, the cylinder has to stop.
Sorry for the late response. I was pleasantly surprised to see Prophet sir's response. Indeed the answer given by him is correct.
We know that during a perfectly elastic collision, the momentum transfered per particle per collision is 2mv_0 while for a perfectly inelastic collision, it is simply mv_0. So initially the resultant force on the right face (where elastic collisions are going on) is greater than that on the left. As a result the cylinder accelerates towards the left. As it gains in speed, the net force on the right face decreases while that on the left face increases. The increase in the force on the right face is due to (i) reduced momentum transfer per particle per collision because the relative speed decreases; and (ii) the reduced number of collisions per second. The force on the left face increases due to the increases in the above mentioned factors.
After some time the forces on the two sides equalize, the acceleration becomes zero and the cylinder then onwards move with a constant speed. Let this speed be v_1.
The net force on the right face is 2m(v_0-v_1)^2nA
Here n = number of particles per unit volume and A = area of the face of the cylinder.
On the other hand, on the left face the net force is m(v_0+v_1)^2nA
Since these are equal. So
(v_0+v_1)^2=2(v_0-v_1)^2\ \Rightarrow v_0+v_1=\pm\sqrt{2}(v_0-v_1)
Disregarding the negative sign (Why?) we obtain the required speed of the cylinder after a long time as
v_1=\dfrac{\sqrt{2}-1}{\sqrt{2}+1}\ v_0
but how.........
i am so intrigued by this question...
kaymant sir pls dont keep us in the dark....i am too curious to know the answer............
yes the ans by theprophet sir is correct
i forgot to consider the change in frequency of collision
@eureka, the cylinder will of course move towards the left. However, its velocity after a long time won't be the same as the rebounding particles.
Since the collisions from the right are elastic, the particles will bounce back with opposite velocity.
and particles from the left will, in effect, stop.
The net motion after the collisions must be of particles to the right (bouncing back), and, from conservation of momentum, the cylinder to the left.
Eventually the cylinder will be moving at the same velocity as the rebounding particles, but to the left.
sir can u pls give some hint as to what u mean by long time and very long time.......?
if we assume that infinite small particles strike from right and left....then i keep getting the answer as 0
sir do we assume that the mass of the cylinder M is >>> m (mass of each particle) ?