PARADOXES in EM theory ??

starter

If two protons are moving at a speed v relative two you through space in the same direction and are separated by a small distance, you will see them exert a magnetic force upon each other, because they are essentially two currents running in the same direction. However, if you are moving along with the protons at speed v, such that they appear to you as stationary, you would measure only an electrostatic force pushing them apart. So how could it be that two protons will attract each other in one frame of reference yet repel in another?

Good one

E&M Paradox

I first read about this apparent paradox in QED and the Men Who Made It: Dyson, Feynman, Schwinger, and Tomonoga by Silivan S. Schweber. Feynman was presented the puzzle while at Los Alamos during WWII (by Ted Welton, a friend he kept a joint physics notebook with while an undergraduate at MIT.) Be warned, it took Feynman all night to solve this:

--------------------------------------------------------------------------------

(from The Feynman Lectures on Physics, Vol. II sec. 17-4)

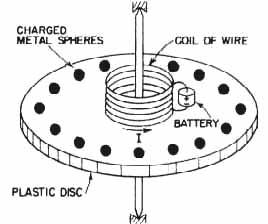
Imagine that we construct a device like that shown in the figure. There is a thin, circular plastic disc supported on a concentric shaft with excellent bearings, so that it is quite free to rotate. On the disc is a coil of wire in the form of a short solenoid concentric with the axis of rotation. This solenoid carries a steady current I provided by a small battery, also mounted on the disc. Near the edge of the disc and spaced uniformly around its circumference are a number of small metal spheres insulated from each other and from the solenoid by the plastic material of the disc. Each of these small conducting spheres is charged with the same electrostatic charge Q. Everything is quite stationary, and the disc is at rest. Suppose now that by some accident-or by prearrangement-the current in the solenoid is interrupted, without, however, any intervention from the outside. So long as the current continued, there was a magnetic flux through the solenoid more or less parallel to the axis of the disc. When the current is interrupted, this flux must go to zero. There will, therefore, be an electric field induced which will circulate around in circles centered at the axis. The charged spheres on the perimeter of the disc will all experience an electric field tangential to the perimeter of the disc. This electric force is in the same sense for all the charges and so will result in a net torque on the disc. From these arguments we would expect that as the current in the solenoid disappears, the disc would begin to rotate. If we knew the moment of inertia of the disc, the current in the solenoid, and the charges on the small spheres. we could compute the resulting angular velocity.

But we could also make a different argument. Using the principle of the conservation of angular momentum, we could say that the angular momentum of the disc with all its equipment is initially zero, and so the angular momentum of the assembly should remain zero. There should be no rotation when the current is stopped. Which argument is correct? Will the disc rotate or will it not? We will leave this question for you to think about.

We should warn you that the correct answer does not depend on any nonessential feature, such as the asymmetric position of a battery, for example. In fact, you can imagine an ideal situation such as the following: The solenoid is made of superconducting wire through which there is a current. After the disc has been carefully placed at rest, the temperature of the solenoid is allowed to rise slowly. When the temperature of the wire reaches the transition temperature between superconductivity and normal conductivity, the current in the solenoid will be brought to zero by the resistance of the wire. The flux will, as before, fall to zero, and there will be an electric field around the axis. We should also warn you that the solution is not easy, nor is it a trick. When you figure it out, you will have discovered an important principle of electromagnetism.