Another old trick

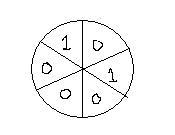
It is a problem of invariance

let a,b be two adjacent elements

after carrying out the operation they become
a+1,b+1

now, there are three sectors in the whole circle .

hence if we consider a and b as a part of one sector .

we get the summation of difference between the two elements of each subset=
a+1-b+1+..=a-b+...=unchanged

if we consider a and b part of different sectors

we get still

x-(a+1)+b+1-y+...=a-b+...=unchanged

when all the elements will be equal then the sum will be =0+0+0=0

but initial sum=1-0+1-0+0-0=2
but it should be invariant
..

hence CONTRADICTION ..