21@ iitimcumin MEthd PLease
Three rods of identical cross sectional area are made up of same metal from the sides of an isosceles triangles ABC, right angled at B. The point A and B are maintained at temperatures T and √2T respectively.
In the steady state, the temperature of the point C is TC. Assuming that only heat conduction takes place
Tc/T=
-
UP 0 DOWN 0 0 10
10 Answers
3HEAT COMIN IN = HEAT FLOWIN OUT .............
LETS TAKE POINT B .............
k(√2T - T) = k(Tc - √2T)
2√2T - T = Tc
2√2 - 1 = Tc/T ........
NOT VERY SURE ..........
1Tc/T=1
heat flow from A to B = heat flow from A to C + heat flow from C to B
simplifying u will get
(√2T - T )/a = (Tc - T)/√2a + (√2T - Tc )/a
u will get Tc = T ..
106
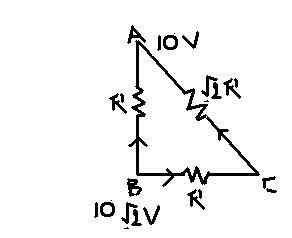
using electrical analogy... VA = 10 (=T degree) VB = 10√2 .. RAB = R = RBC, RAC = R√2
Let current be i... through RAB.. and i' through RBAC
VC/10 ... is required anser..
So, 10(√2-1) = iR ... (i)
10(√2-1) = i'R(√2+1) .... (ii)
==> (√2+1)i' = i .... (dividing (i) and (ii)) ..
Now, 10√2 - VC = i'R = [i/(√2-1)]*[10(√2-1)/i]
==> VC = 10(√2-1)
So, VC/10 = √2-1
OR TC/T = √2-1
1This Q cud be solved using nishant sir's post in conduction 3 post
It is also ∞ 1/x
Total heat transferred =k A (Tc - T) / √2 x + k A (Tc - √2 T ) / x
In steady state it is eaual to 0...
Solving it Tc/ T = 3 /√2 - 1 = 3(√2 -1)
