if theta will be big the restorig torque will nt be linear.so no shm only periodic..if theta is small it will be shm
1.We know that the formula for time period for a simple pendulum is
2pi√(l/g).While deriving the formula we say that Theta is small so sin Theta is aproximately =theta.Thus the formula is valid for small oscillations.
Now another proof,
let us consider the SHM to be a linear SHM
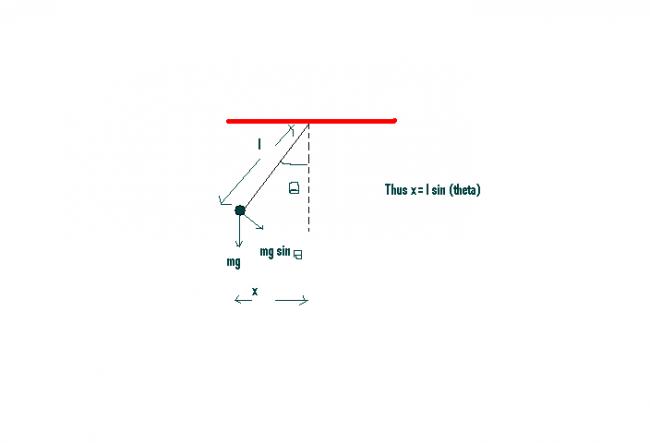
Thus from figure,
x= l sin (theta)......1
Frestoring=mg sin(theta)
From 1,sin(theta)=x/l
Thus ,Frestoring=mgx/l=mw^2x, i.e w=√g/l
Threfore,T=2 pi √l/g.
Here, we did'nt use any aproxiimation like theta is small.So, the formula is valid for all values of theta (big or small !) or is it???
-
UP 0 DOWN 0 0 5

5 Answers
u r still doing approximations ,
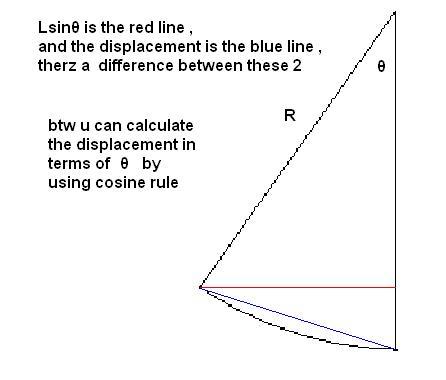
ur displacement is Lθ , not Lsinθ
so u unknowningly approximated sinθ≈θ
@querty
Here x=l sin(theta) and x is the displacement from mean position.