39thanks dude.
that was good work by the way
A copper and a tungsten plate having a thickness of 2 mm each are riveted together at 00C to form a bimetallic strip.
Find the average radius of curvature of this plate at 2000C
The coefficients of linear expansion for copper and tungsten are
1.7*10-5 and.4*10-5 K-1 respectively
-
UP 0 DOWN 0 2 2
2 Answers
11
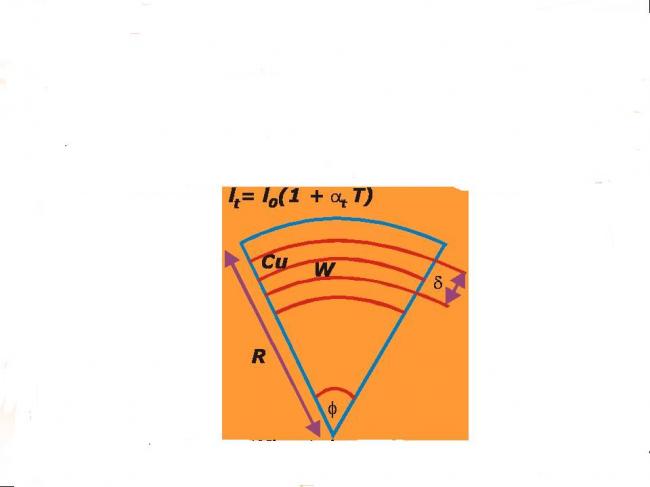
The avg length of copper plate at a temp T=200 ° C is
l c = l0 (1 + @ c T)
where l 0 is the length of cu plate at 0 ° C
The length of Tungsten plate is l t = l 0 (1 + @ t T)
We shall assume that the edges of plates are not displaced during deformation and that inc in the plate thickness due to heating can be neglected.
From the figure we have,
l c = Φ (R + δ/2 ) and similarily
l t = Φ(R - δ/2 )
Here δ is the thickness
Consequently,
Φ(R + δ/2) = l0 (1 + @ c T)...............(1)
Φ(R = δ/2 ) = l0 (1 + @ t T) ................(2)
Dividing (1) by (2) ; we get
(R + δ/2)(R - δ/2 ) = (1 + @ c T)(1 + @ t T)
Therefore, we get
R = δ [2 + (@c + @t ] T
[2(@c - @t)T]
Therefore, R = δ(@c - @t) T neglecting (@c +@ t) in the numerator. Substituting the values above we get
R = 2 mm / (2.3 x 10-5) (200 +273) = 0.769 m