36This can also be proved as follows................
2 Answers
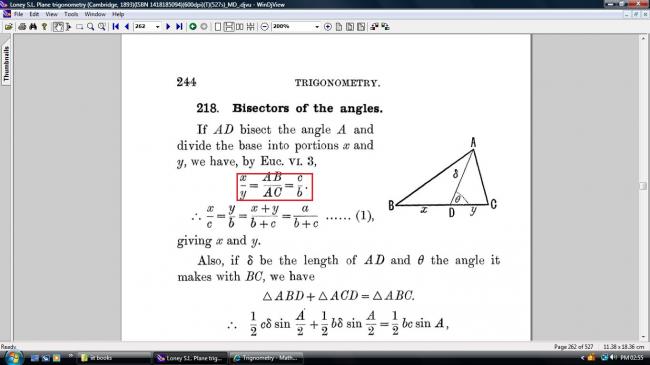
341That is the angle bisector theorem.
An easy way to see this is by looking at the ratios of the areas of \bigtriangleup{ABD} and \bigtriangleup{ADC} in two ways.
Since the altitudes are equal, they are in the ratio of the bases i.e x:y
Again \bigtriangleup{ABD} = \frac{1}{2} c \delta \sin \frac{A}{2} and \bigtriangleup{ADC} = \frac{1}{2} b \delta \sin \frac{A}{2}
giving the ratio as c:b
