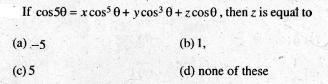11
11Ans ) Here, cos 5 θ = x cos 5 θ + y cos 3 θ + z cos θ
Differentiating w.r.t θ , we get
-5 sin 5 θ = x (5 cos 4 θ) (-sin θ) + y (3 cos 2 θ ) (-sin θ) - z sin θ
Putting θ = pie / 2, we get
-5 sin 5 pie2 = - z sin pie/2
Therefore, z = 5
Hence ans is (c) [1]
 1
1hey i guess this is not a good way to solve this q
wat abt if u were asked abt x y also
use demoviers theorem
(cosθ +isinθ)n=cos(nθ)+isin(nθ)=expansion of (cosθ +isinθ)n binomially
then equate real parts of lhs and rhs and imaginary parts of lhs and rhs....
u ill get the ans