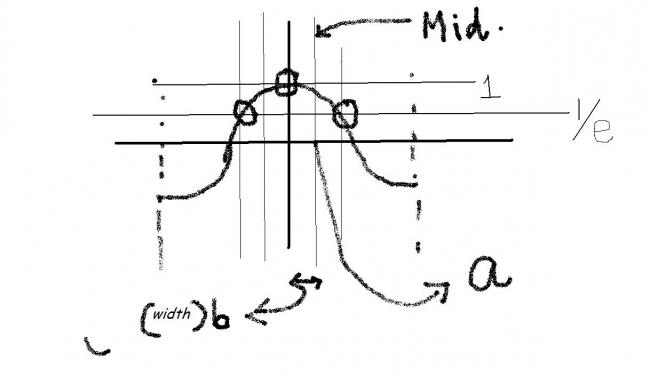
i think e is exponent...
it was asked in jee 2005
the number of ordered pairs (a,b) where a,b belongs to (-Ï€,Ï€) satisfying cos (a-b) =1 and cos (a+b) =1/e will be ???????????
-
UP 0 DOWN 0 0 12

12 Answers
skygirl
·2009-02-05 07:14:56
a-b = 0 (a-b cant be taken 2pi ,,,, then a has to greater than 2pi which is not possible)
and a+b = cos^-1 (1/e) and 2pi-cos^-1 (1/e) both
then we get two pairs.
Manish Shankar
·2009-02-05 09:43:20
yeah it will be 4
a=b
so cos(2a)=1/e
2a=2nπ±cos-1(1/e)
a=nπ±(1/2)cos-1(1/e)
so a=±(1/2)cos-1(1/e), π-(1/2)cos-1(1/e), -π+(1/2)cos-1(1/e)