1hmm... i see... but this is not very easy to do..
i mean how can i gt this kind of a solution in the exam.. is there not a conventional way of solving this same quesiton...
i mean by derivatives etc..??
solve: 2sinx=|x| +a
find a such that there is no real root!
-
UP 0 DOWN 0 0 3
3 Answers
62This is a very good problem.
We assume that f(x)=2 sinx
g(x) = |x|+a
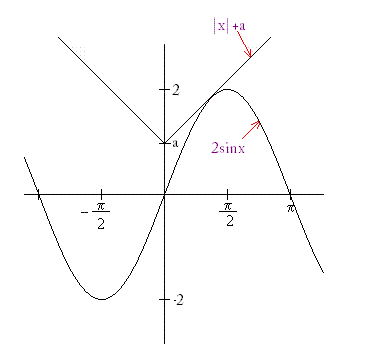
a is from the graph
when both will just touch, df(x)/dx=dg(x)/dx
we take positive x only.(if u draw the graph, it becomes evident why!) If it does not ask me i will tell u...
taking derivative at that point where they touch,
so, 2cos h = 1 cos h =1/2
again from graph, it is evident that h is less than pi/2
so h=pi/3
now a=f(x)-|x|
so, at this point, a =2sinx-|x| = √3- pi/3!
1
33Graphical method is very convinient method of solving a prob and 4 ur question a>√3-Pi/3 4 no real root