OHH.. I DIDT SEE .. SORRY ....
WELL THIS MIGHT SEEM ILLOGOCAL TO FEW PEOPLE BUT I KNOW THAT MOST OF THEM DONNO THIS. BUT VERY USEFUL IN SOME PROBLEMS.
in a triangle ABC, angle bisector of A, AD is drawn. what is lengthof AD? {of course in terms of a,b,c ,A,B,C}
if any of 11thies proves it, then well and gud.
and ya, how many of u didnt know this before please do post here
`i didnt knew`
-
UP 0 DOWN 0 1 28

28 Answers
arrey all these are the same
just that each has its own time of use :)
but b555, wats the use of this formula... as sky(formerly) and now (star) said apollonius is better and anyways this can be found out in little time...
ek baat kahu tum sabse??
if u remember apollonius' theorem, no need of even angles...
jus u need to know the ration in which AD cuts BC.
oh ya thx bhaiyya ... kabhi kabhi itni chhoti chhoti batein dimaag mein nahin ghusti hain
@asish..
it is the same solution as bhargav's
See closely
ab sin C = bc sin A
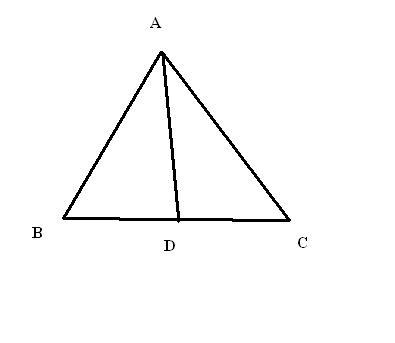
Maine kiya:
from angle bisector theorem,
AB/AC = BD/DC
==> c/b=BD/DC
==> (c+b)/b = a/DC
==> DC=ab/(c+b) ... (i)
in ΔADC,
DC/sinA/2 = AD/sinC
==> DC = ADsinA/2/sinC ... (ii)
equating (i) and (ii) and solving...
AD = absinC/(b+c)sin(A/2)
now absinC = bcsinA
so, AD = bc.2sin(A/2)cos(A/2)/(b+c)sin(A/2)
==> AB = 2bccos(A/2)/(b+c)
I DID LIKE THIS ..... LET IT DIVIDE BASE IN RATIO M:N .......
M:N = c/a ......
n = a2 /(c+a) ...
sinA/2 / n = sinC / AD ........
PLS POINT OUT FLAW IN MAH METHOD ................
is it ...
AD = absinC/[sin(A/2)(b+c)] ???
abhi derive kiya tha...
Please give the solution , i have tried it alot but i am unable to get it
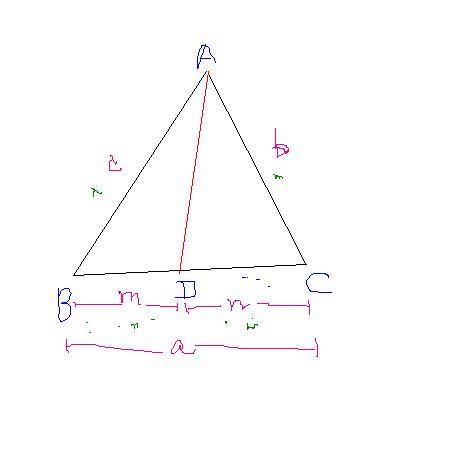
m:n = c:b
by appollonius' theorem...
nc2 + mb2 = nBD2 + mDC2 + (m+n)AD2
(donno if am correct)
nahiin didi, we only know a,b,c ,A,B,C. thats it. there is only one formula and works in all cases.
tell me jus one thing about the question....
i sthis the whole question ??
i mean no more ration or something is given ??